Transtibial amputation prosthetic-users are at risk of developing deep tissue injury (DTI) while donning their prosthesis
for prolonged periods; however, no study addresses the mechanical loading of the residuum during sitting with a
prosthesis. We combined MRI-based 3D finite element modelling of a residuum with an injury threshold and a muscle
damage law to study risks for DTI in one sitting subject in two postures: 30°knee-flexion vs. 90°knee-flexion. We
recorded skin-socket pressures, used as model boundary conditions. During the 90°knee-flexion simulations, major
internal muscle injuries were predicted (.1000mm3). In contrast, the 30°knee-flexion simulations only produced minor
injury (,14mm3). Predicted injury rates at 90°knee-flexion were over one order of magnitude higher than those at 30°
knee-flexion. We concluded that in this particular subject, prolonged 90°knee-flexion sitting theoretically endangers
muscle viability in the residuum. By expanding the studies to large subject groups, this research approach can support
development of guidelines for DTI prevention in prosthetic-users.

Keywords: pressure ulcer; patient-specific finite element model; tissue injury threshold; below-knee prosthesis; amputation rehabilitation

1. Introduction

Transtibial amputation (TTA) prosthetic-users frequently suffer injuries in their residual limb during daily activities (Kosasih and Silver-Thorn 1998; Lyon et al. 2000; Baars et al. 2008). The soft tissues of the residuum are unnaturally compressed and deformed between the hard prosthetic socket and the truncated tibia and fibula bones, which promotes pressure ulcers (Salawu et al. 2006). The elevated temperature (Peery et al. 2005), humidity and sometimes vacuum conditions (Beil et al. 2002) inside the socket further amplify the danger of development of pressure ulcers. Multiple studies measured limb–socket surface pressures in this context, during different activities such as standing up from a chair or walking (Zhang and Roberts 2000; Sanders et al. 2005). These studies assumed that high surface pressures endanger the integrity of the residual limb. This assumption is logical when concerning surface abrasions and other skin injuries, but proved inaccurate when concerning injuries developed in deep tissues near bony prominences. In recent patient-specific finite element (FE) simulations (Portnoy et al. 2008, 2009a), we showed that elevated internal mechanical strains and stresses in the soft tissues of the residuum may lead to deep tissue injury (DTI) in the distal tibial end during an upright standing position. In contrast to superficial pressure ulcers that onset at the skin surface and that are easily identifiable, DTI is a dangerous lesion that may progress undetected in internal soft tissues. A DTI initiates in skeletal muscle tissue at the proximity of sharp or curved bone edges (Ceelen et al. 2008; Stekelenburg et al. 2008; Black 2009; Gefen 2009; Oomens et al. 2010). The main catalysts for the onset and rapid escalation of a DTI are localised, elevated mechanical strains and stresses in muscle tissue, which are applied for prolonged durations (Ceelen et al. 2008; Oomens et al. 2010). Quantification of the loads and time exposures to loads which cause irreversible muscle damage was obtained by means of animal studies (Linder-Ganz et al. 2006) and tissue-engineered model systems (Gefen et al. 2008) of DTI. These studies consistently indicated that the tolerance of living muscle tissue to compressive loads decreases sigmoidally with time, in a manner which can be described mathematically using an exponentially decreasing Boltzmann function (Gefen 2010). An algorithm coupling the muscle injury threshold obtained in the animal studies of Linder-Ganz et al. (2006) with a tissue damage law (associating injury with localised abnormally altered tissue mechanical properties) was previously utilised to predict risks for DTI in the buttocks of paraplegic patients, based on local soft tissue stresses and time exposures to stresses (Gefen 2007; Linder-Ganz and Gefen 2009).

Similarly to patients confined to wheelchairs or beds, whose impaired sensory system does not alert them to the danger of DTI, prosthetic-users may also suffer sensory impairments (neuropathy) due to diabetes or vascular disease complications, or nerve severance caused by the TTA itself (Kosasih and Silver-Thorn 1998). Accordingly, neuropathic TTA patients may not shift loads in their residuum as frequently as non-neurologically impaired amputees (who can sense discomfort or pain signals); therefore, enabling initiation of DTI in the neuropathic residuum.

In a recent publication, we presented five subjectspecific three-dimensional (3D) FE models of TTA residual limbs under static load bearing in a standing-like posture (Portnoy et al. 2009a). In these simulations, we identified two subjects who were theoretically prone to DTI if they were to load their residuum continuously while standing for more than 3 h (Portnoy et al. 2009a). Loading a residual limb during standing without relieving the loads for 3 h is, however, unlikely in real-world situations. Conversely, continuous loading of the residuum inside the prosthetic socket while sitting is a common routine. A prosthetic-user may sit for hours on long flights, in a train, in the cinema or even when falling asleep in front of the television before taking off the prosthesis. Despite the predominance of the sitting posture, especially in TTA prosthetic-users, there are no data in the literature describing the biomechanics of the residuum during static sitting. In particular, there is a paucity of information regarding internal stresses in the soft tissues of the residuum during sitting. The results of our previous work, studying the internal mechanical state of the TTA residuum during standing and walking (Portnoy et al. 2008, 2009a, 2009b, 2010), suggest that the danger of DTI in the residuum of a seated TTA prosthetic-user might have been overlooked in the literature, as sitting with a prosthesis might involve sustained tissue deformations in the residuum for potentially long time periods.

The likelihood of a condition where the residuum is confined inside the prosthetic socket during prolonged sitting motivated us to study the risk of DTI in this common daily state for TTA individuals. We particularly expect that gaining knowledge of high-risk sitting postures may provide important guidelines for prosthetic-users, particularly for those who suffer from neuropathy. Accordingly, we hypothesise that (1) the residual limb of TTA prostheticusers is at risk of DTI during prolonged sitting and (2) the risk of DTI during sitting is posture dependant. The objective of this study was to present a method and case study to test these hypotheses. Specifically, we aimed at simulating DTI in the residual limb of a TTA prosthetic-user, seated in two different postures, by coupling patient-specific FE modelling, muscle injury threshold and a tissue damage law.

A traumatic unilateral TTA male prosthetic-user (age 55 years, weight 73 kg, 4 years since the TTA) participated in this study. The amputated limb was the right limb (residuum length 11.5 cm, tibial length 10.9 cm, fibular length 9.4 cm). The subject reported holding an active lifestyle and attested to using his prosthesis for at least 5 h a day. Additionally, he suffered no lesions or pain in his residuum. Helsinki approval (#4302/06 from Sheba Medical Center, Ramat-Gan, Israel) and informed consent were obtained before the trial. For this subject, we measured pressure distributions between the residuum and prosthetic socket during sitting (Figure 1(a)). We used a previously described pressure measurement system which includes two thin (0.3 mm) and flexible pressure-sensing mats designed specifically for surface pressure measurements around a TTA residuum inside a prosthetic socket (Portnoy et al. 2008). Briefly, this system was designed by our Musculoskeletal Biomechanics Laboratory and Sensor Products Co. (Madison, NJ, USA) according to anthropometric data of lengths and circumferences of residual limbs of TTA individuals (Sanders et al. 2005). A Tshaped mat with 175 pressure sensors enveloped the posterior aspect of the shin and a second, long rectangle mat with 150 pressure sensors was placed at the anterior aspect of the residuum and then folded over its distal end (Figure 1(b)). The area of each sensor is 1.024 cm² and its measurement capacity is ,700 kPa. The accuracy, repeatability, hysteresis and nonlinearity of sensors are ±10, ±2, ±5 and ±1.5%, respectively. Data were sampled at 19Hz and then processed using commercial software (Tactilus, version 3.1.12, Sensor Products Co.).

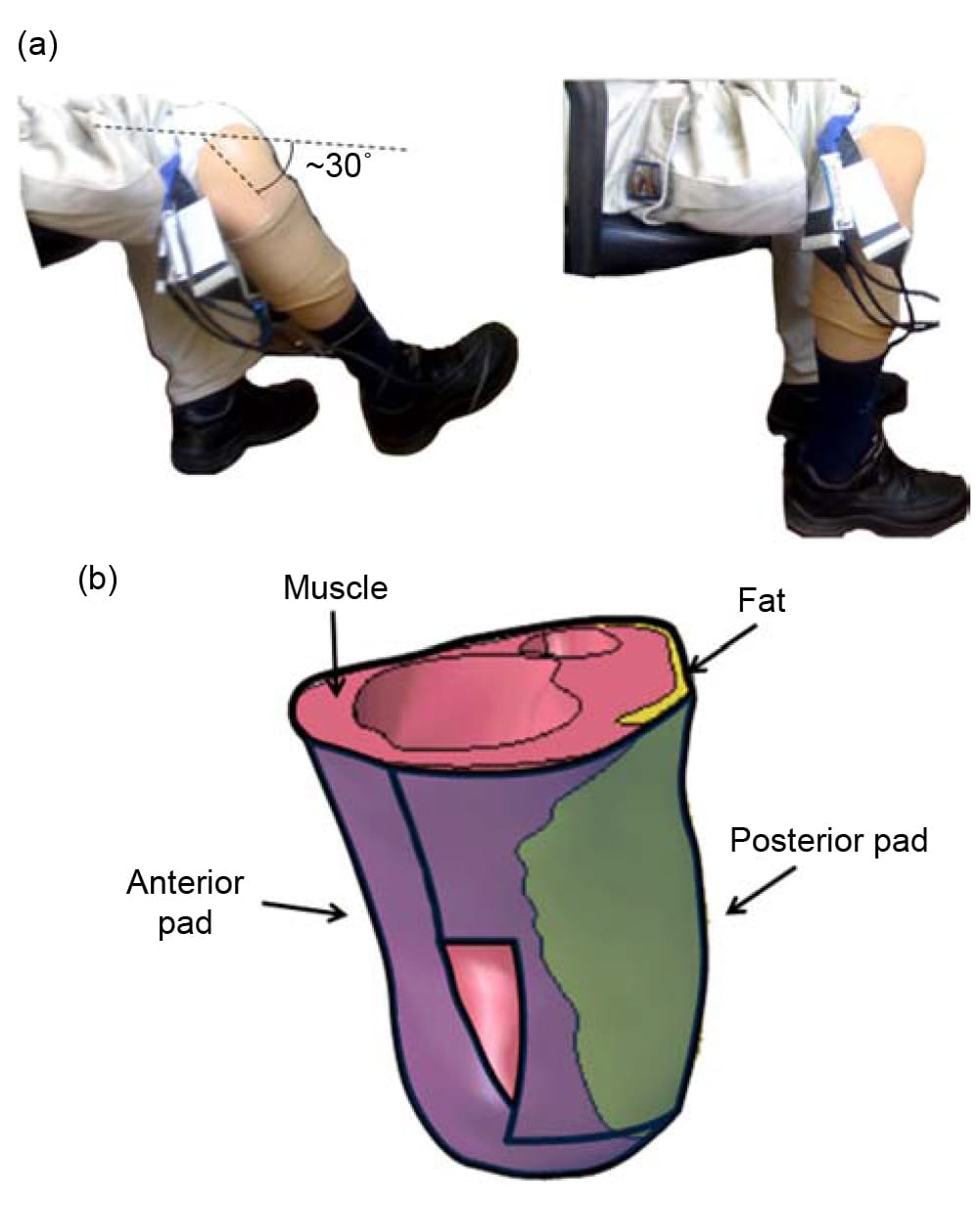
Figure 1. The experimental design: (a) The subject was seated in two different postures, of 30°-knee-flexion (left frame) or 90°-knee-flexion (right frame). (b) A long rectangle pressure sensor pad was located at the anterior and inferior aspects of the residuum. A T-shaped pressure sensor pad was located at the posterior aspect of the residuum.

Together, the pads covered the residuum very well, with just a slight overlap at the distal corners of the posterior T-shaped pad (Figure 1(b)). Additionally, because the thin, flat and flexible cabling of the T-shaped pad passes through one of its distal corners, it might have produced localised measurement noise at that corner. We, therefore, averaged pressures measured just at that corner of the T-shaped pad with its surroundings to smooth any potential artefacts.

The pressure-sensing mats were placed directly on the skin of the residuum. The subject then rolled up his sock on top of the pressure mats and donned his prosthesis. The interface pressure measurements were obtained during two sitting postures: first, while the subject sat comfortably with his residual limb stretched forward in a ,30° knee flexion and second, while the subject sat on the same chair, maintaining a 90°knee-flexion (Figure 1(a)). Pressure data in the 30°-knee-flexion sitting trial were recorded for a duration of over 1min. During the 90°-knee-flexion sitting, the subject complained that he sensed high pressures to his residuum and data recording, therefore, terminated sooner, after approximately 30 s when the subject reported that he felt considerably uncomfortable. An average 3D surface pressure distribution on the residuum was obtained for each sitting posture (local pressure fluctuations over time were small, below 5 kPa, for both postures).

Our method for acquiring the 3D subject-specific anatomy of the TTA residuum for FE analyses is thoroughly described in our recent publications (Portnoy et al. 2008, 2009a, 2009b), where FE studies were conducted in order to quantify internal mechanical conditions in the soft tissues of TTA prosthetic-users during standing-like load-bearing posture. For completeness, this method will be described shortly herein. We created a knee-high plaster cast replica of the residuum which was used as a non-metallic substitute for the prosthetic socket, while the subject was scanned in an upright posture inside an open-MRI (field intensity 0.5 T, spatial resolution 0.1 mm, slice thickness 4 mm, images were T1-weighted, phase field-of-view 100%, ‘Signa SP’ model, General Electric Co., Fairfield, CT, USA). The plaster cast was gently resting on the MRI table for stability, but the subject was instructed not to apply any load onto his residuum.

We built 3D bodies of the truncated tibia and fibula, the muscle flap and fat tissue in the residuum using the coronal and axial MRI scans by means of a solid-modelling software (SolidWorks 2009, SolidWorks, Concord, MA, USA). The 3D bodies were then imported to an FE solver (ABAQUS v6.8, Simulia, Providence, RI, USA; Figure 2) for nonlinear large deformation stress analyses. A 1-mmthick skin layer was added on the external surface of the residuum using the FE pre-processor. Bones were assumed to behave as rigid surfaces (as they are orders of magnitude stiffer than all soft tissues), and soft tissues were all assumed to be hyperelastic, homogeneous and isotropic. The soft tissues were modelled using the generalised Mooney–Rivlin solid strain energy function (Mooney 1940):

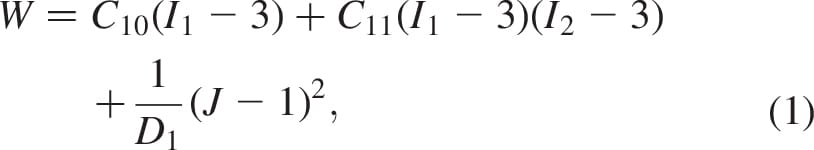
where the invariants of the principal stretch ratios 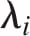are 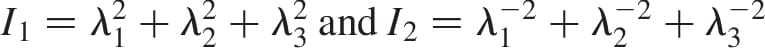, the relative volume change is 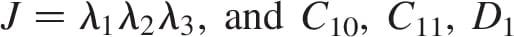, are the constitutive parameters, specified in Table 1.

Tissue volumes in the FE residuum model and the properties of its mesh (Figure 2) are provided in Table 2. The mesh density (Figure 2; Table 2) was tested in preliminary simulations, where it was found that denser meshes increased the runtime for a stress analysis (which was approximately 6 h of analysis using three processors on a Linux-operated Intel core I-7, 2.66 GHz computer) but had negligible effect on calculated soft tissue stress data. We assumed ‘no-slip’ conditions at all tissue-on-tissue contact surfaces. The proximal soft tissues at the knee joint were constrained for mediolateral and posterior–anterior movements. The measured 3D surface pressures (Figure 3)were applied to the external surfaces of the residuum model at two separate simulation configurations: sitting with 30° knee flexion and with 90° knee flexion (Figure 3). The FE processor calculated Green-Lagrange strains and second Piola Kirchhoff stresses, and then converted stress data to Cauchy stresses, which is the stress measure used in the algorithm described below.

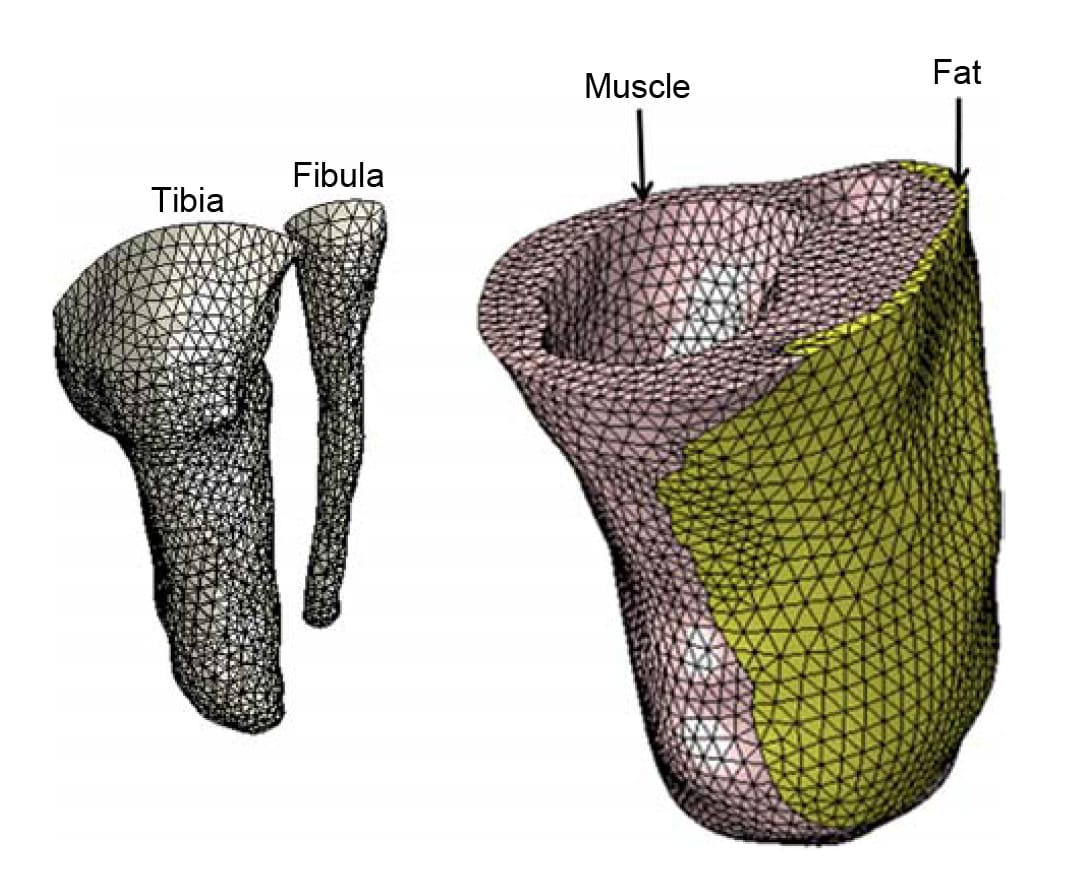
Figure 2. The FE mesh of the residuum models. The model comprises the truncated bones: the tibia and fibula (left frame) and the soft tissues of the residuum: muscle, fat and skin (right frame).

A well-established algorithm for DTI simulations, previously used by Gefen (2007) and Linder-Ganz and Gefen (2009) for theoretical studies of DTI risk factors in paraplegic patients was utilised herein for the TTA prosthetic-user case. This algorithm essentially combines FE modelling with empirical injury threshold and damage law for muscle tissue subjected to sustained loading. The injury threshold for muscle tissue was adopted from Linder-Ganz et al. (2006) who formulated a relationship between the compression stress level that cause irreversible damage to muscle tissue (s) and the time of exposure to this stress (t), based on histopathology data from animal studies

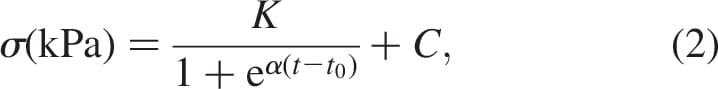
where K = 23 kPa, a = 0.15 min^-1, t₀ = 95 min and C ¼ 8 kPa (Linder-Ganz et al. 2006). Muscle regions which surpass the critical stress s (Equation (2)) are expected to be permanently damaged. Muscle damage involves localised tissue stiffening at the injured sites which has been observed in animal studies (Linder-Ganz and Gefen 2004; Gefen et al. 2005) as well as in patients (Gefen 2009). Hence, the stiffer injured lesions may affect the loading state of their surroundings by projecting elevated stresses to nearby uninjured tissues. Measurements of the altered mechanical properties of injured muscle tissue were published by Gefen et al. (2005):

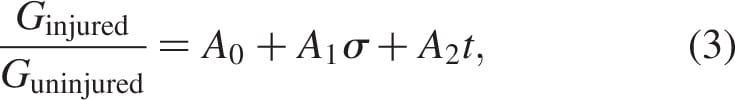
where G_injured and G_uninjured are the long-term shear moduli of the injured and uninjured muscle tissues, respectively, and the empirical constants are A₀ = 0.742, A₁ = 0.022 kPa^-1 and A₂ = 0.012 min^-1.

For each of the two models representing the two sitting postures (30° and 90° knee flexions), five time-step simulations were performed in order to eventually compare the theoretical risks for DTI during prolonged sitting with a TTA prosthesis between the two postures. In these simulations, we increased the time step in 15-min intervals to simulate the evolution of internal stresses in the soft tissues of the residuum over a total period of 75 min. We chose to simulate the development of internal stresses within a time frame in the order of an hour since TTA individuals who use a prosthesis are relatively active (as opposed to paraplegia) so a state of static sitting without relieving the loads in their residuum beyond 1 h is unlikely, even in the presence of neuropathy. After each increase in time step, we created an output report file from ABAQUS containing identification and compression stress data of all the muscle elements in which compression stresses exceeded the injury threshold (Equation (2)). This output report file along with the last created ABAQUS input file was read by a designated code (LabView 8, National Instruments, Austin, TX, USA) that assigned updated mechanical properties to the muscle elements predicted to be injured (Equation (2)), using the empirical damage law given in Equation (3). The code regenerated an ABAQUS-readable input file for the next time step simulation, in which stress data in the soft tissues of the residuum were recalculated considering the stiffening of each damaged muscle element. This process was hence repeated five times per each sitting posture (Figure 4). Outcome measures included predictions of the time-dependent volume of simulated damaged muscle tissue for each sitting posture, as well as the respective rate of progression of tissue damage in cubic millimetre per minute.

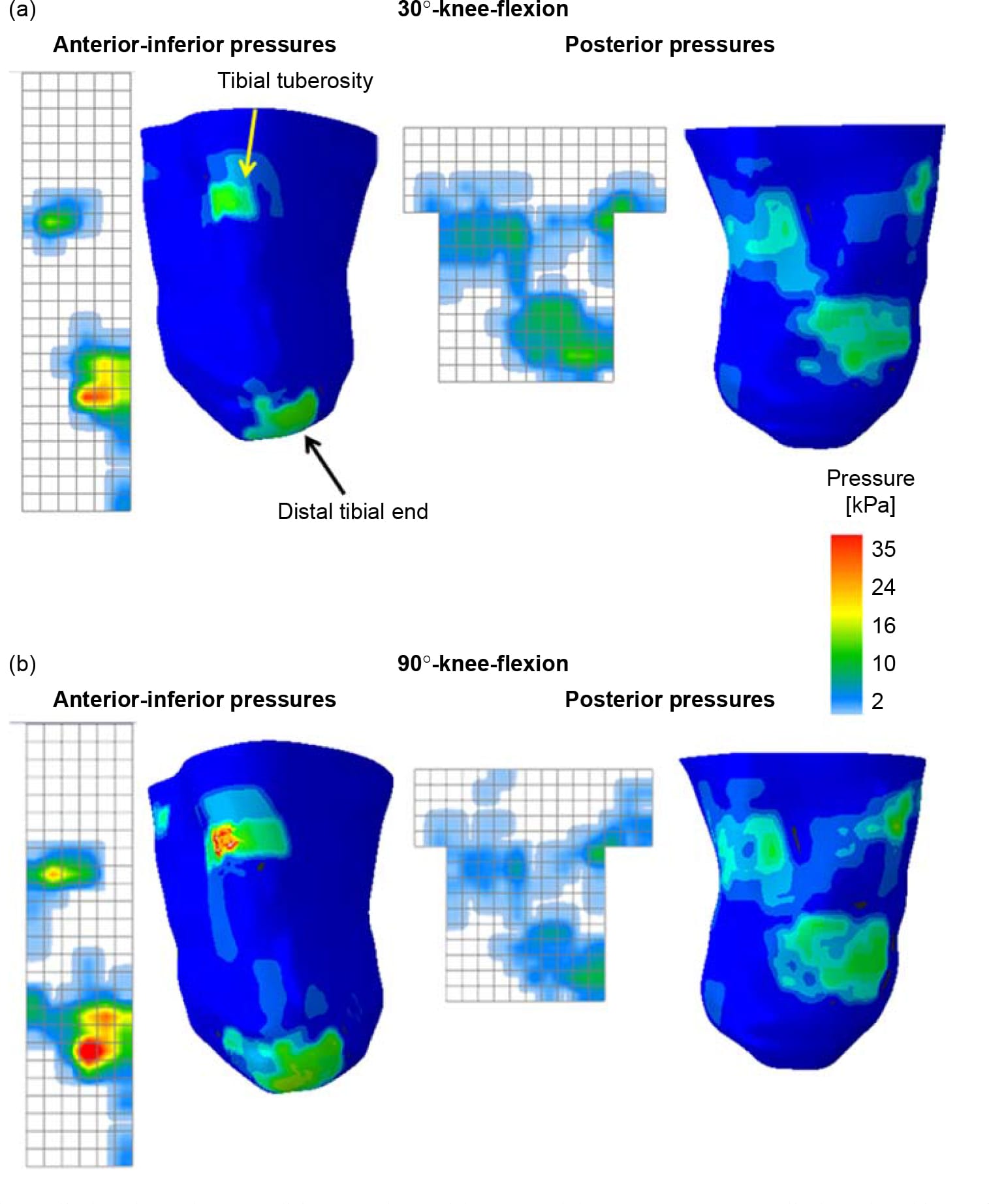
Figure 3. The loads applied as boundary conditions to the residuum models are pressures, applied to the skin surface according to pressure measurements taken while the subject sat in (a) 30°- and (b) 90°-knee-flexion sitting postures.

For both sitting postures (30° and 90°knee flexions), the maximal surface pressures were located mainly at the distal tibial end and the tibial tuberosity, as measured by the anterior pad, and also on top of the gastrocnemius belly, as measured by the posterior pad (Figure 3).

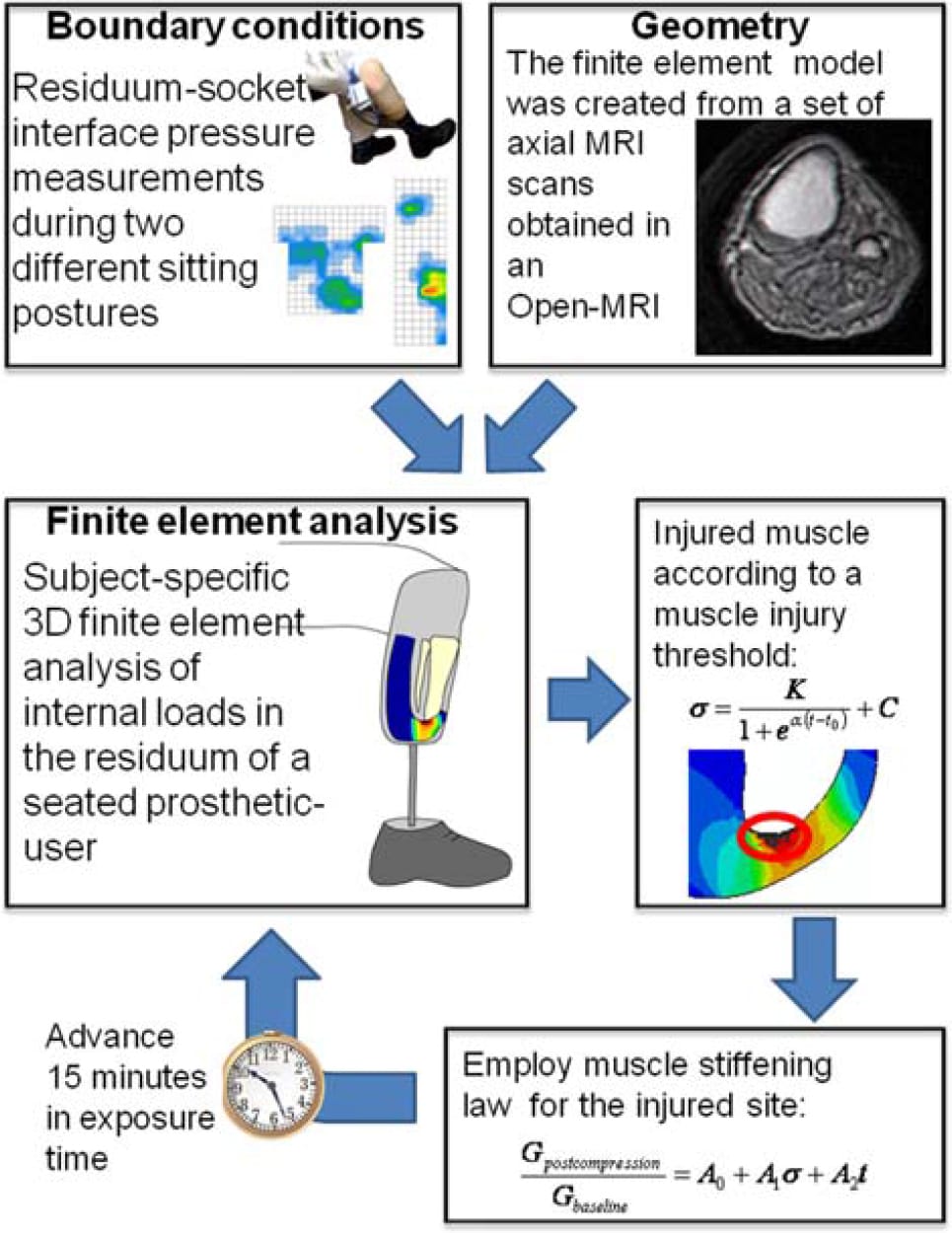
Figure 4. The iterative algorithm used in this study is to simulate the progression of DTI in a patient-specific FE model of the residuum of a seated TTA prosthetic-user. In each iteration, the volume of injured muscle tissue is calculated using an injury threshold that was previously obtained from experimental studies in animal models (Equation (2)). The injured tissue volume is then locally stiffened in the model using an empirical damage law for muscle tissue (Equation (3)). The time step is then increased and a new iteration begins.

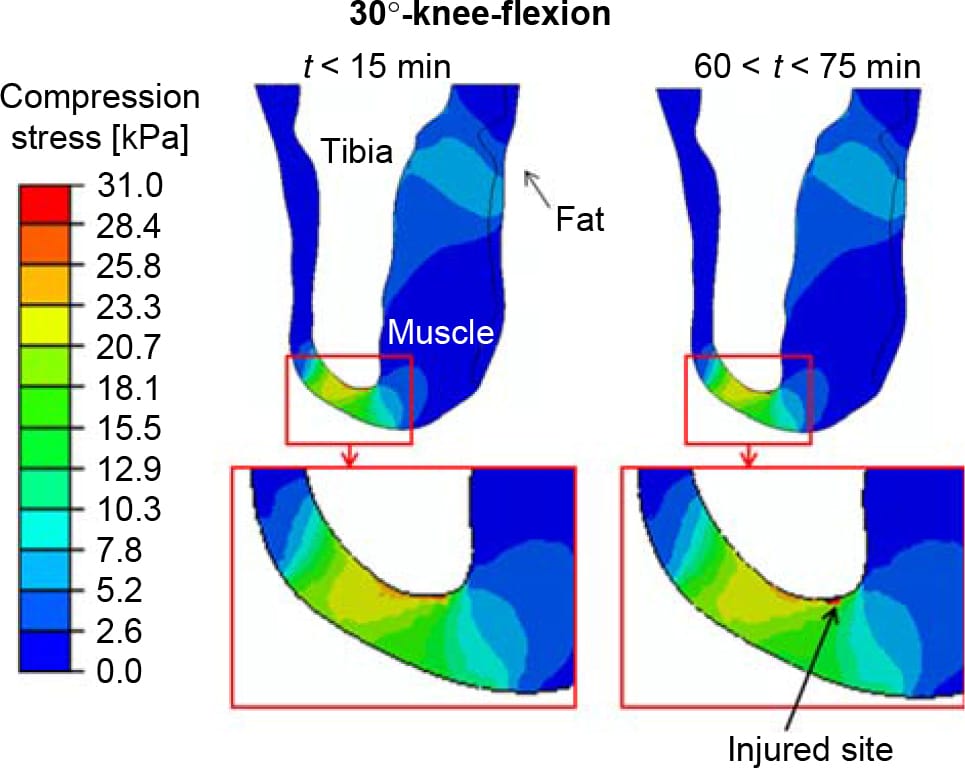
Figure 5. The distribution of compression stresses (kPa) in a sagittal cross-section through the tibia during the first 15 min and at times 60 < t < 75 min, calculated for a sitting posture of 30°-knee-flexion. Only extreme time points are shown since the differences between solutions for subsequent 15-min intervals were negligible. The region under the distal tibial end is magnified for each time point, for clarity. The injured site in muscle tissue is marked with an arrow.

The distributions of compression stresses in the residuum during continuous immobilised sitting are shown in Figure 5 for sitting with 30°knee-flexion and in Figures 6 and 7 for sitting with 90°-knee-flexion. Predicted muscle injuries are superimposed on these stress diagrams as black spots. Numerical data of maximal compression, tension and shear stresses in muscle tissue at the simulation time points that correspond to these stress diagrams are provided in Table 3. During the 30°-knee-flexion sitting, there were no potential injuries predicted at the tibial tuberosity, and there was only slight muscle damage, not exceeding 14mm3 in size at all simulation times, at the distal tibial end (Figure 5). This negligibly small simulated damage did shift the stress distribution in the surrounding muscle tissue slightly, but not to an extent that promoted more substantial simulated damage over the 75-min simulation period (Figure 5). In stark contrast, the 90°- knee-flexion sitting caused rapidly escalating simulated damage to muscle tissues, at both the distal tibial end and tibial tuberosity sites, where tissue thicknesses were 6.4 and 5.2 mm, respectively (Figures 6 and 7).A3Dcapture of the predicted locations and sizes of injured muscle tissues in the residuum while sitting with the prosthesis continuously and with no movement for over an hour with the knees flexed to 90° is presented in Figure 8.

The maximal principal compression and tension stresses, the maximal shear stress and the von Mises stress in muscle tissue all increased with time, excluding the case of principal tension stresses near the tibial tuberosity for 90°knee-flexion sitting, where maximal stresses fluctuated around a steady level (Table 3). For the 90°knee-flexion sitting, maximal principal compression stresses in muscle tissue near the distal tibial end were approximately twofold higher than in muscle tissue around the tibial tuberosity. The maximal principal tension stress, maximal shear stress and von Mises stress at the distal tibial end during 90°knee-flexion sitting were approximately threefold higher than the corresponding stresses at the tibial tuberosity in the same posture. The maximal stresses at the distal tibial end were approximately twofold higher in 90°knee-flexion sitting compared to those in 30°knee-flexion sitting (Table 3).

The time-dependent volumes of injured muscle tissue are quantified separately in Figure 9 for the two sitting postures and per each injured location (distal tibial end and tibial tuberosity). The predicted total injured muscle volume was consistently over an order of magnitude greater for sitting with the knees flexed at 90° than for 30°, throughout the entire time course of simulations (Figure 9). For example, during the first 15 min of continuous immobilised sitting with the prosthesis, the size of the predicted injury for 90°knee-flexion sitting was 1002mm3 (distal tibial end and tibial tuberosity injuries taken together), compared to only 12.6mm3 in total for the 30°knee-flexion sitting (Figure 9). For the 90°kneeflexion sitting, the tibial tuberosity injury was predicted to be mildly larger in volume than the injury at the distal tibial end (there was a ,8% size difference averaged across time; Figure 9). The rates of progression of the simulated injuries in cubic-millimetre of damaged muscle tissue per minute are provided in Table 3. Rates were greater for the 90°knee-flexion sitting than for 30°-knee-flexion by at least an order of magnitude. Moreover, while the slight simulated injury that developed in the 30°knee-flexion sitting posture progressed at a nearly constant, slow rate (,0.015mm3/min), injuries which developed at the 90°knee-flexion simulations progressed fast over the first 30 min and then rates were stabilised (Table 3; Figure 9).

In this study, we utilised a well-established algorithm (Figure 4; Linder-Ganz and Gefen 2004, 2009; Gefen 2007; Nagel et al. 2009) that couples subject-specific FE modelling with an injury threshold and a damage law for muscle tissue (Gefen et al. 2005), in order to simulate the onset and progression of DTI in a residual limb of a TTA prosthetic-user, seated at two different postures (Figure 1(a)). Our purpose was to present a case study which emphasises the importance of neuropathic prosthetic- users’ awareness to the position of their limb during prolonged stationary conditions. Since neuropathic amputees may not change their posture as frequently as nonneuropathic amputees, they are more likely to suffer DTI.

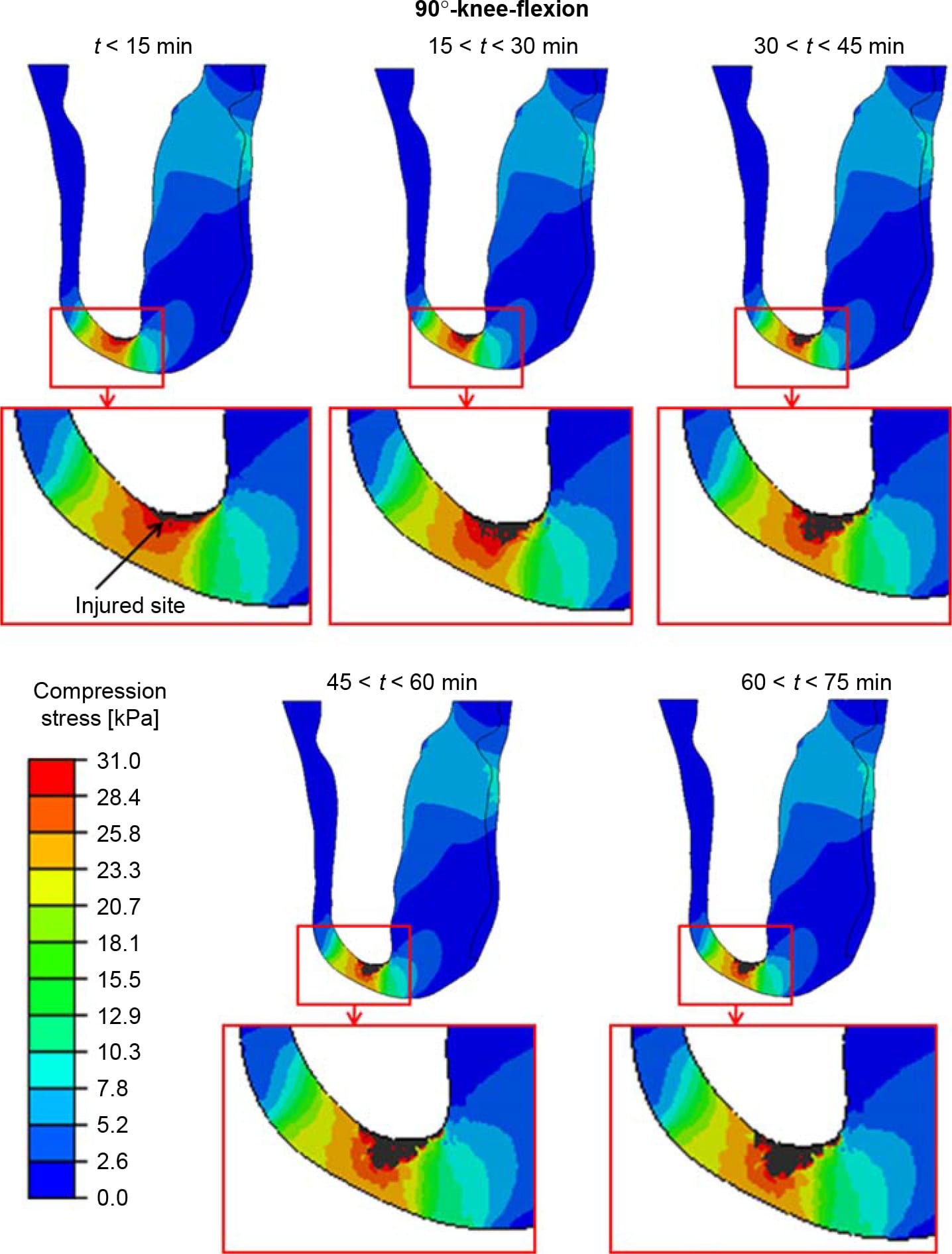
Figure 6. The distributions of compression stresses (kPa) in a sagittal cross-section through the tibia during time intervals of 15 min, calculated for a sitting posture of 90°-knee-flexion. The region under the distal tibial end is magnified for each time point, for clarity. The injured site in muscle tissue is marked with an arrow.

We ended our analyses after 75 min of simulated sitting since TTA individuals who use a prosthesis are relatively active, so that a state of entirely immobilised sitting for more than an hour is unlikely, even in the presence of neuropathy. Additionally, model-predicted injury rates at all the injured locations were high during t , 30 min, but then either decreased towards a steadystate (for 90°knee-flexion sitting) or kept steady (for 30°knee-flexion) for the remaining simulation period, 30 < t < 75 min (Table 3; Figure 9).

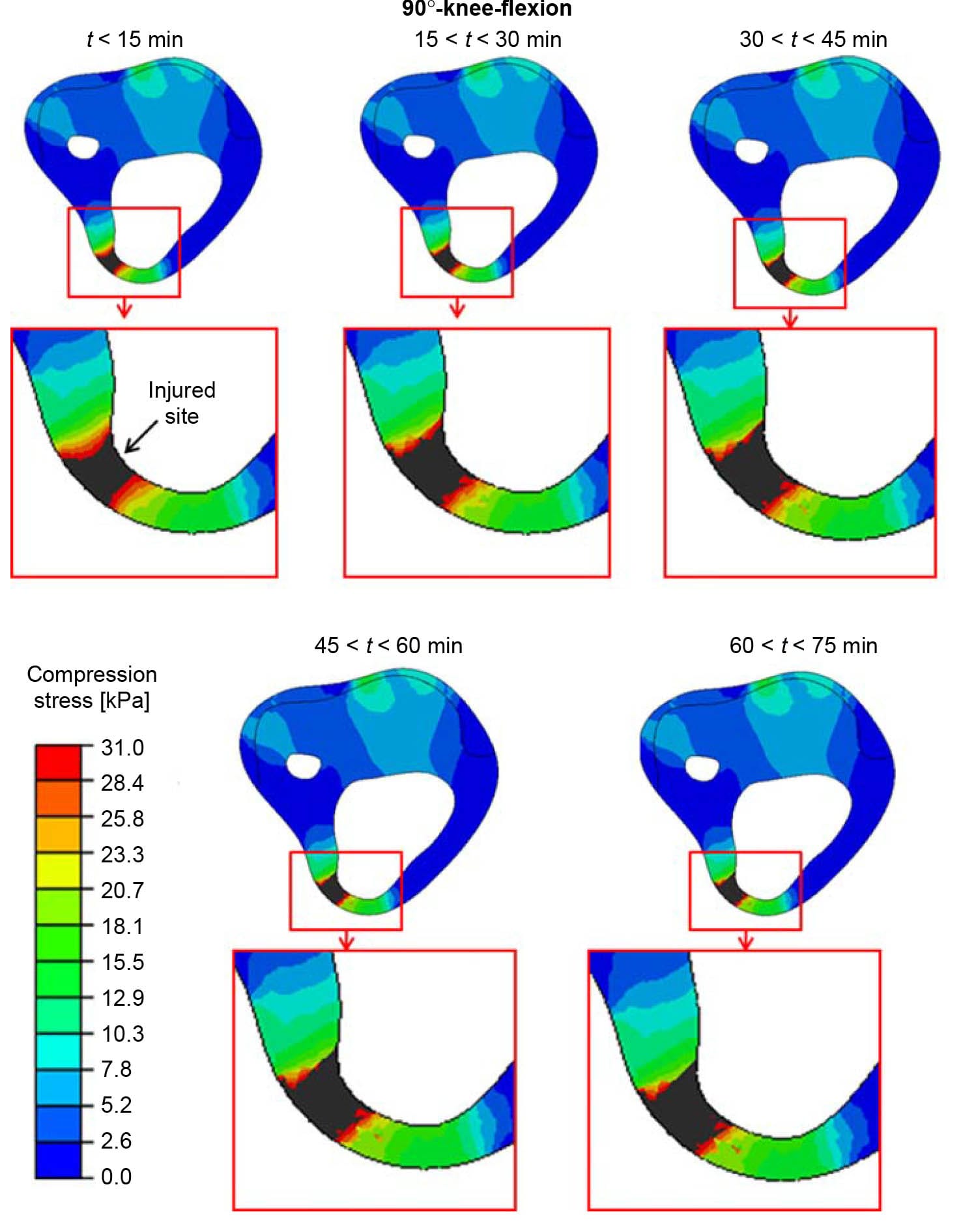
Figure 7. The distributions of compression stresses (kPa) in an axial cross-section through the tibial tuberosity during time intervals of 15 min, calculated for a sitting posture of 90°-knee-flexion. The region around the tibial tuberosity is magnified for each time point, for clarity. The injured site in muscle tissue is marked with an arrow.

The present results supported our hypotheses, as our FE simulations showed that the TTA residuum is theoretically at risk for DTI during sitting, and also that the risk for DTI is posture dependant. Generally, we found that the muscle volumes predicted to be injured were substantially larger when simulating sitting with the prosthesis so that the knees are flexed to 90°, compared to 30° knee flexion (Figure 9). This finding indicates that theoretically, during prolonged sitting, a DTI is more likely to irrupt in the residuum at higher knee flexion angles. Adding to this conclusion is our finding that the injury rate at 90°knee-flexion is over one order of magnitude higher than the injury rate at 30°knee-flexion (Table 3; Figure 9). The relative swiftness in which the simulated DTI progressed in the 90°knee-flexion sitting model further demonstrates the dangerous nature of this injury, which is known to develop unnoticeably over such short time periods (Gefen 2008).

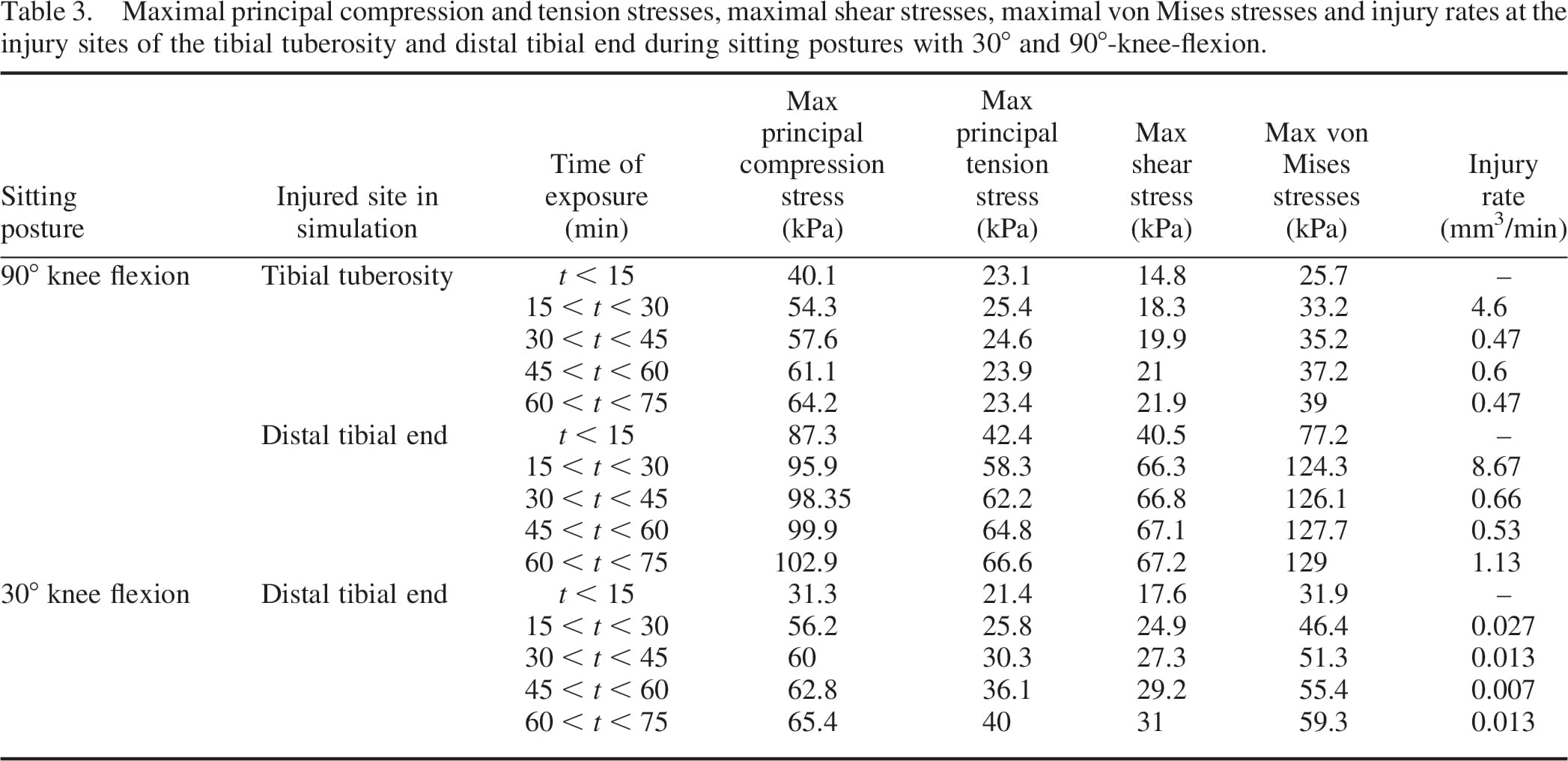
The muscle tissues adjacent to the tibial tuberosity were not injured when simulating sitting with 30°kneeflexion. As measured by the pressure mats (Figure 3), pressures over the tibial tuberosity during 30°knee-flexion sitting were lower than the corresponding pressures generated while the subject sat with his knees flexed to 90°. The tibial tuberosity pressures for 30°knee-flexion were associated with muscle compression stresses below the injury threshold (Equation (2)) at that site throughout the entire simulated period, theoretically holding no danger for a tibial-tuberosity-located DTI for the present subject during the 1-h of sitting. During sitting with the knees flexed at 90°, the predicted injured muscle volume at the tibial tuberosity was predicted to be mildly larger for the subject, with respect to the injured muscle volume at the distal tibial end (Figure 9). This was probably caused by the thinner soft tissue padding at the tibial tuberosity site (,20% thinner tissue layer). The rate of progression of the muscle injury during the 90°knee-flexion sitting was, however, greater for the distal tibial end than for the tibial tuberosity (Table 3; Figure 9), which might be associated with the higher maximal compression stresses accumulated in muscle tissue around the tibial end for this sitting posture (Table 3).

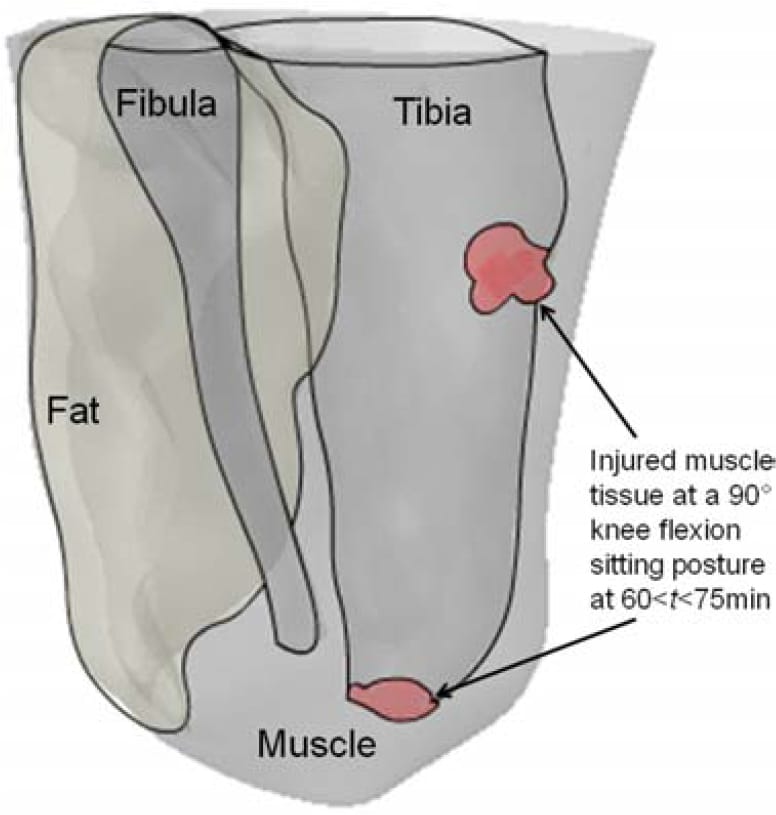
Figure 8. A 3D capture of the predicted muscle tissue injuries at the distal tibial end and the proximity of the tibial tuberosity, for a sitting posture of 90°-knee-flexion at times 60 < t < 75 min.

When analysing the 90°knee-flexion sitting posture, we found that the simulated injury at the tibial tuberosity, where the tissue padding was thinner, initiated as an hourglass-shaped injury (Figure 7; Ohura et al. 2007). In the clinical setting, this condition would have probably been diagnosed on sight as a severe grade-IV pressure ulcer. Conversely, in the proximity of the distal tibial end, the model-predicted injury initiated at the bone proximity and did not reach the skin surface after 75 min of simulated sitting (Figure 6). This finding alerts to the prime danger of DTI, which is its ability to sometimes remain hidden in subdermal tissues and silently spread without breaking the skin. In our simulations, the injured muscle volume at the distal tibial end increased during the 90°knee-flexion sitting by almost 40% within 1 h of sitting (Figure 9), during which the compression stresses at the skin proximity remained below the injury threshold (Figure 6).

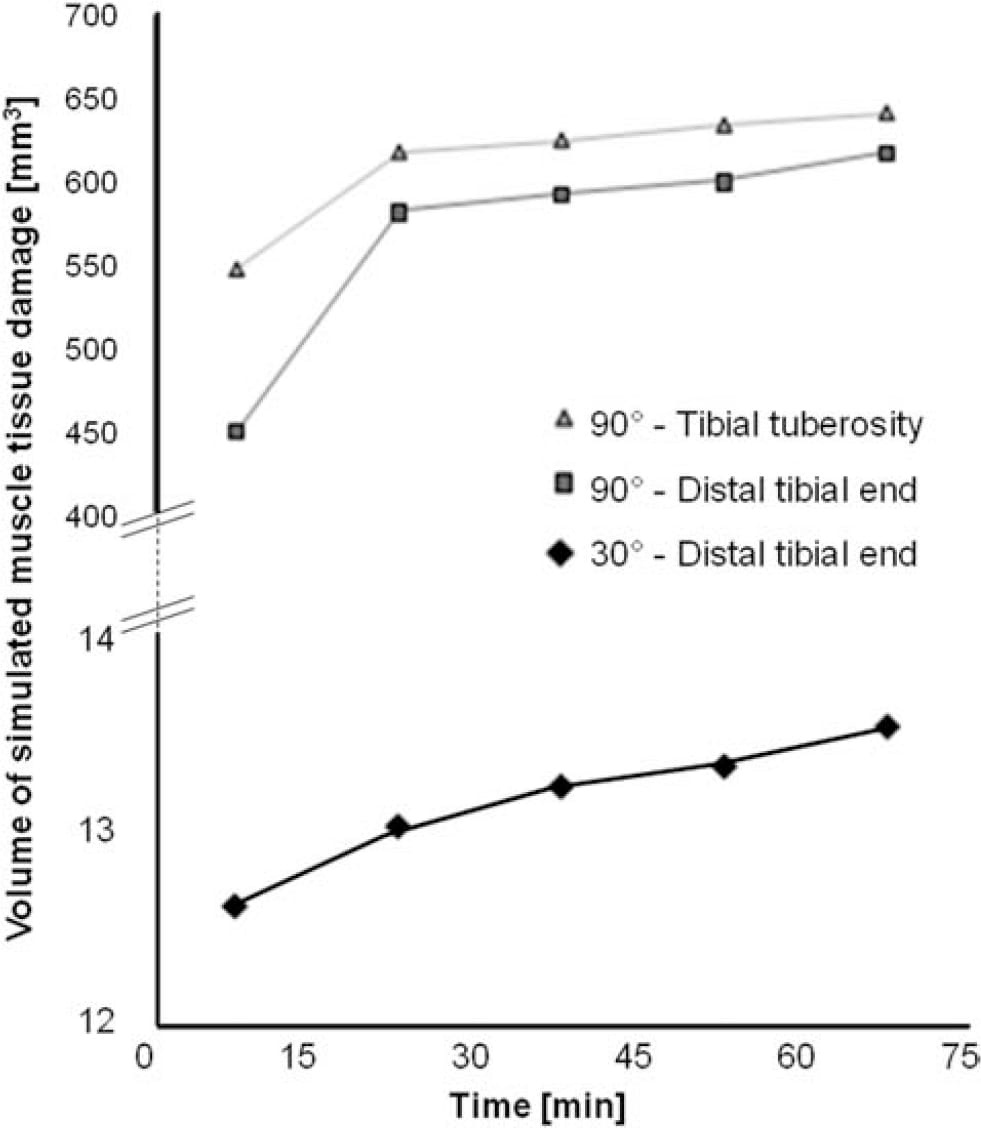
Figure 9. The volume of simulated muscle tissue damage vs. time, for sitting postures of 30° and 90°-knee-flexion. Volumes of simulated muscle damage are plotted separately for the distal tibial end (squares for 90°-knee-flexion, diamonds for 30°-kneeflexion) and the proximity of the tibial tuberosity (triangles; 90°-knee-flexion).

The outcomes of our FE simulations herein are subjectspecific, derived from the actual anatomy of a residual limb of an individual TTA prosthetic-user. There is, however, a wide range ofvariation betweenTTAresidual limbs, in terms of the geometries of the truncated bones and overlying soft tissues (e.g. in bone lengths and distal end bevelments) as well as in soft tissue composition and layer thicknesses. The mechanical properties of soft tissues in the residuum also vary across patients, as a result of biological variability but also depending on age, level of activity and presence of scars and diseases that affect collagen organisation, such as diabetes. These factors were investigated in an earlier study using subject-specific FE modelling,where effects of factors on the internal mechanical state in the residual limb were isolated and quantified (Portnoy et al. 2009b). The von Mises stresses calculated in a spastic muscle tissue, for example, were elevated twofold when compared to flaccid muscle tissue (Portnoy et al. 2009b). Theoretically, the impact of a twofold increase in stresses due to prolongedmuscle spasms can be roughly estimated from the stress distribution presented in Figure 6, for 90°knee-flexion sitting. Looking at the colour-coded stress scale in Figure 6, it can be estimated that this contraction-induced twofold increase in stresses would create a skin-breaking hourglass-shaped injuryunder the distal tibial end (similarlytothat simulated at the tibial tuberosity in Figure 7) during as early as the first 15 min of the static immobilisation accompanied by spasm. Considering the predicted injuredmuscle volumeat the distal tibial end after 75 min of immobilised 90°knee-flexion sitting (Figure 9), it can be deduced that such skin-breaking DTI which is associated with spasm would spread to substantially larger tissue volumes than the one seen in Figure 6.

The main limitation of this study is that the injury threshold (Equation (2)) and damage law (Equation (3)) for skeletal muscle tissue were derived from a rodent model (Gefen et al. 2005; Linder-Ganz et al. 2006), since animal studies are the only feasible means to obtain such data. A second limitation is the measurement of residuum– socket interface pressures alone, without accounting for shear stresses at the interface, which might have altered the internal stress distribution pattern to some extent. Unfortunately, incorporating hardware for shear measurements across the entire 3D surface of the residuum is not yet feasible technologically, as shear transducers, even when optimally integrated into the socket, cannot fully envelop the entire residuum as simply as the pressure-sensing mats do. Another limitation arises from the mechanical properties assigned to muscle tissue, which were extracted from healthy animal studies (Table 1). Despite the publication of several human studies which measured mechanical properties of the TTA residuum bulk using indentation (Vannah et al. 1999; Gefen and Dilmoney 2007; Schwartz et al. 1998), we chose to assign properties extracted from an animal model in order to distinguish between muscle and fat, rather than considering them together as one effective material. An additional limitation is the absence of connective tissues in our FE models. This assumption, however, is reasonable since during TTA the lower third of the shin, which includes the tendons, is amputated (Schwartz et al. 1998). Another factor that was not taken into account in our model is the temperature of the residuum which documented fluctuations (Peery et al. 2005) and which might influence ulcer formation. Last, we used ‘tie’ connections at all tissue-on-tissue interfaces, in the absence of experimental data characterising the relevant coefficients of friction. In view of the limitations addressed above and potential other ones, we recommend that the present data regarding sizes and time courses of DTI be interpreted as trends of effects, rather than as absolute values. With that being said, we believe that the considerable differences between calculated risk measures (extents and rates of injury) of sitting with 30°knee-flexion vs. 90°knee-flexion clearly point to the potential risk that the latter sitting posture involves for TTA patients.

In conclusion, we presented a biomechanical case study which combines patient-specific 3D FE modelling of a TTA residuum with an injury threshold and a damage law for skeletal muscle, in order to test the risk for DTI during prolonged sitting with a prosthesis in two sitting postures: 30°knee-flexion vs. 90°knee-flexion. Our results identified the 90°knee-flexion sitting as a posture that theoretically endangers muscle tissue viability in the residual limb of this particular subject, if unrelieved for a long period. The present study, therefore, highlights the use of biomechanical modelling as a tool for identifying postures that endanger the residuum. Additionally, the present method can be utilised to study the effects of various prosthetic factors, e.g. socket materials and shape rectifications, on internal soft tissue stresses.

This work was partially supported by the Chief Scientist’s Office of the Ministry of Health, Israel (Grant #3-2028, AG), and by the Internal Research Fund at Tel Aviv University (AG).

1. Baars EC, Dijkstra PU, Geertzen JH. 2008. Skin problems of the stump and hand function in lower limb amputees: a historic cohort study. Prosthet Orthot Int. 32:179–185.
2. Beil TL, Street GM, Convey SJ. 2002. Interface pressures during ambulation using suction and vacuum-assisted prosthetic sockets. J Rehabil Res Dev. 39:639–700.
3. Black J. 2009. Deep tissue injury: an evolving science. Ostomy Wound Manage. 55:4.
4. Ceelen KK, Stekelenburg A, Loerakker S, Strijkers GJ, Bader DL, Nicolaij K, Baaijens FPT, Oomens CWJ. 2008. Compresion-induced damage and internal tissue strains are related. J Biomech. 41:3399–3404.
5. Gefen A. 2007. Risk factors for a pressure-related deep tissue injury: a theoretical model. Med Biol Eng Comput. 45: 563–573.
6. Gefen A. 2008. How much time does it take to get a pressure ulcer? Integrated evidence from human, animal, and in vitro studies. Ostomy Wound Manage. 54:26–35.
7. Gefen A. 2009. Deep tissue injury from a bioengineering point of view. Ostomy Wound Manage. 55:26–36.
8. Gefen A. 2010. Mathematical functions and their properties as relevant to the biomechanical modeling of cell and tissue damage. J Appl Biomech. 26:93–103.
9. Gefen A, Dilmoney B. 2007. Mechanics of the normal woman’s breast. Technol Health Care. 15:259–271.
10. Gefen A, Gefen N, Linder-Ganz E, Margulies SS. 2005. In vivo muscle stiffening under bone compression promotes deep pressure sores. J Biomech Eng. 127:512–524.
11. Gefen A, van Nierop B, Bader DL, Oomens CW. 2008. Straintime cell-death threshold for skeletal muscle in a tissueengineered model system for deep tissue injury. J Biomech. 41:2003–2012.
12. Kosasih JB, Silver-Thorn MB. 1998. Sensory changes in adults with unilateral transtibial amputation. J Rehabil Res Dev. 35:85–90.
13. Linder-Ganz E, Engelberg S, Scheinowitz M, Gefen A. 2006. Pressure-time cell death threshold for albino rat skeletal muscles as related to pressure sore biomechanics. J Biomech. 39:2725–2732.
14. Linder-Ganz E, Gefen A. 2004. Mechanical compression induced pressure sores in rat hind-limb: muscle stiffness, histology and computational models. J Appl Physiol. 96:2034–2049.
15. Linder-Ganz E, Gefen A. 2009. Stress analyses coupled with damage laws to determine biomechanical risk factors for deep tissue injury during sitting. J Biomech Eng. 131: 011033-1–011033-13.
16. Lyon CC, Kulkarni J, Zimerson E, VanRoss E, Beck MH. 2000. Skin disorders in amputees. J Am Acad Dermatol. 42: 501–507.
17. Mooney M. 1940. A theory of large elastic deformation. J Appl Phys. 11:582–592.
18. Nagel T, Loerakker S, Oomens CWJ. 2009. A theoretical model to study the effects of cellular stiffening on the damage evolution in deep tissue injury. Comput Meth Biomech Biomed Eng. 12:585–598.
19. Ohura T, Ohura N, Oka H. 2007. Incidence and clinical symptoms of hourglass and sandwich-shaped tissue necrosis in stage IV pressure ulcers. Wounds. 19:310–319.
20. Oomens CW, Loerakker S, Bader DL. 2010. The importance of internal strain as opposed to interface pressure in the prevention of pressure related deep tissue injury. J Tissue Viabil. 19:35–42.
21. Palevski A, Glaich I, Portnoy S, Linder-Ganz E, Gefen A. 2006. Stress relaxation of porcine gluteus muscle subjected to sudden transverse deformation as related to pressure sore modeling. J Biomech Eng. 128:782–787.
22. Peery JT, Ledoux WR, Klute GK. 2005. Residual limb skin temperature in trans-tibial sockets. J Rehabil Res Dev. 42: 147–154.
23. Portnoy S, Siev-Ner I, Shabshin N, Kristal A, Yizhar Z, Gefen A. 2009a. Patient-specific analyses of deep tissue loads post transtibial amputation in residual limbs of multiple prosthetic users. J Biomech. 42:2686–2693.
24. Portnoy S, Siev-Ner I, Yizhar Z, Kristal A, Shabshin N, Gefen A. 2009b. Surgical and morphological factors that affect internal mechanical loads in soft tissues of the transtibial residuum. Ann Biomed Eng. 37:2583–2605.
25. Portnoy S, van Haare J, Geers RPJ, Kristal A, Siev-Ner I, Seelen HAM, Oomens CWJ, Gefen A. 2010. Real-time subject-specific analyses of dynamic internal tissue loads in the residual limb of transtibial amputees. Med Eng Phys. 32:312–323.
26. Portnoy S, Yizhar Z, Shabshin N, Itzchak Y, Kristal A, Dotan-Marom Y, Siev-Ner I, Gefen A. 2008. Internal mechanical conditions in the soft tissues of a residual limb of a trans-tibial amputee. J Biomech. 41:1897–1909.
27. Salawu A, Middleton C, Gilbertson A, Kodavali K, Neumann V. 2006. Stump ulcers and continued prosthetic limb use. Prosthet Orthot Int. 30:279–285.
28. Sanders JE, Zachariah SG, Jacobson AK, Fergason JR. 2005. Changes in interface pressures and shear stresses over time on trans-tibial amputee subjects ambulating with prosthetic limbs: comparison of diurnal and six-month differences. J Biomech. 38:1566–1573.
29. Schwartz S, Spencer F, Galloway A, Shires G, Daly J, Fischer J. 1998. Principles of surgery. 7th ed. New York: McGraw-Hill. p. 991–999.
30. Stekelenburg A, Gawlitta D, Bader DL, Oomens CW. 2008. Deep tissue injury: how deep is our understanding? Arch Phys Med Rehabil. 89:1410–1413.
31. Vannah WM, Drvaric DM, Hastings JA, Stand JA, III, Harning DM. 1999. A method of residual limb stiffness distribution measurement. J Rehabil Res Dev. 36:1–7.
32. Zhang M, Roberts C. 2000. Comparison of computational analysis with clinical measurement of stresses on below-knee residual limb in a prosthetic socket. Med Eng Phys. 22: 607–612.

Get a free pressure indicator sample for Biomechanics application.