When two objects touch, their contacting surfaces form a plane. The application of force by one of the objects applied over this surface plane results in Contact Pressure, which is measured as force per unit area. Contact pressure is quite difficult to measure directly. As a result, this topic has been extensively studied and reported in the literature of many scientific areas.
The need to accurately measure and model the sliding friction of hydrogels is motivated by the ocular discomfort of contact lens wearers. (Soft contact lenses are made from hydrogels.) Since friction is related to contact pressure between the lens and eye, Alison Rennie¹ developed equations to calculate contact pressure. These equations, which are quite complex, are shown in Figure 1.

Contact Pressure Sensor
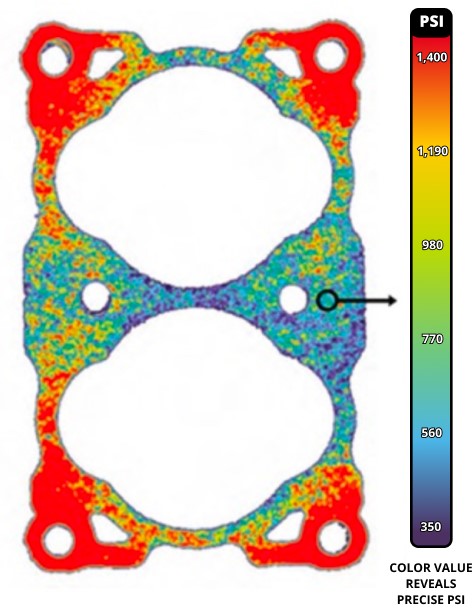
Fig 1: Surface Pressure Distribution of a Gasketed Interface
In other work, Russell, et al² , studied hips using finite element models. They found significant differences between patients with asymptomatic and symptomatic hips. Peak cumulative contact pressure increased as a result of bone irregularities in the hip joint.
Camacho, et al³ , analyzed metal forging operations between flat parallel platens. A finite element model was used to obtain contact pressure distributions. The results show the influence of the boundary conditions on the forces and pressures of the forging process.
Zamponi, et al4 , developed an optimum contact pressure calculation methodology, usable in a computer aided design environment, for aeronautic gear boxes.
Hota V. S. GangaRao and Arshad Vali made determinations of contact pressure distribution between bridge decks and truck tires. This work revealed the following trends:
- Increase in inflation pressure increases the peak values of the contact pressure distribution profile;
- Maximum contact pressure is found to be about 2.5 times the average pressure computed from the current AASHTO specifications for highway bridges;
- The rate of increase in contact pressure is not as rapid as the increase in axle loads;
- Fully treaded tires are found to result in higher contact pressures than the bald tires;
- Load carried by main bars is higher when they are placed perpendicular to, more than parallel to the traffic flow.
As previously stated, contact pressure is difficult to measure directly. In addition, investigative studies, such as those discussed above, are time consuming and too theoretical for many engineers in the manufacturing environment. An excellent alternative for the study of contact pressure is Fujifilm Prescale® Pressure Indicating Film.
Fujifilm Prescale® is a unique, affordable, and easy to use tool that reveals the distribution and magnitude of pressure between any two contacting, mating or impacting surfaces. Pressure indicating sensor film is extremely thin (4 to 8 mils), which enables it to conform to curved surfaces. It is ideal for invasive intolerant environments and tight spaces not accessible to conventional electronic transducers.
Simply place Fujifilm Prescale® between any two surfaces that touch, mate or impact. Apply pressure, remove it, and immediately the film reveals the contact pressure distribution profile that occurred between the two surfaces. Like Litmus paper, the color intensity of the film is directly related to the amount of pressure applied to it. The color intensity increases as the pressure increases.
Fujifilm Prescale® is a very useful tool for engineers needing to obtain contact pressure information on their manufacturing operations.
References
- Alison Rennie, “Measurement and Modeling of Sliding Friction on Soft Curved Surfaces,” Journal of Undergraduate Research, Volume 5, Issue 8, May 2004
- Mary E Russell, Kiran H Shivanna, Nicole M Grosland, and Douglas R Pedersen, “Cartilage contact pressure elevations in dysplastic hips: a chronic overload model,” J Orthop Surg, volume 1, 2006
- A.M. Camacho, M. Marin, E.M. Rubio, and M.A. Sebastian, “Analysis of forces and contact pressure distributions in forging processes by the finite element method,” Annals of DAAAM & Proceedings, Annual, 2005
- L. Zamponi, E. Mermoz, and J. M. Linares, “Contact Pressure Calculation Methodologies in Aeronautic Gearboxes in the CAD Process,” The Future of Product Development, 2007, ISBN 978-3-540-69819-7 (Print) 978-3-540-69820-3
- Hota V. S. GangaRao and Arshad Vali, “Truck-Tire Steel Grid Deck Contact Pressure Distributions,” Journal of Structural Engineering, Vol. 116, No. 3, March 1990, pp. 791-808