Xinbao Yang, A.M.ASCE1; Jun Wei2; Antonio Nanni, F.ASCE3; and Lokeswarappa R. Dharani4
1Structural Engineer, Modjeski and Masters, Inc., 804 North First St., St. Louis, MO 63102 (corresponding author). E-mail: [email protected]. 2Research Assistant, Dept. of Mechanical Engineering, Univ. of Missouri-Rolla, Rolla, MO 65409. 3Jones Professor, Center for Infrastructure Engineering Studies, Univ. of Missouri-Rolla, Rolla, MO 65409. 4Professor, Dept. of Engineering Mechanics and Aerospace Engineering, Univ. of Missouri-Rolla, Rolla, MO 65409. Note. Discussion open until March 1, 2005. Separate discussions must be submitted for individual papers. To extend the closing date by one month, a written request must be filed with the ASCE Managing Editor. The manuscript for this paper was submitted for review and possible publication on January 23, 2003; approved on June 5, 2003. This paper is part of the Journal of Composites for Construction, Vol. 8, No. 5, October 1, 2004. ©ASCE, ISSN 1090-0268/2004/5-444–451/$18.00.
Abstract: At present, fiber reinforced polymer (FRP) composite materials are extensively used to strengthen concrete structures and a main application is wrapping compression members such as building and bridge columns for improved strength and ductility. In this case, FRP laminates are intended to provide confinement to the concrete and the cross section shape plays an important role on the effectiveness of the method. The primary purpose of this paper is to introduce a test device and a test method designed to determine the effect of corner radius on the strength of the FRP laminate and on the distribution of the resulting radial stress on the substrate material. Various curvatures were investigated. In the proposed device, they can be realized by using interchangeable inserts. Strain distribution around the corner, failure load, and failure mode of the FRP laminate were monitored and analyzed. The stress concentration in the laminate is studied numerically using the finite element method and compared with experimental results. The relationship between radial stress distribution and corner radius is determined to provide guidance in practical cases.
DOI: 10.1061/(ASCE)1090-0268(2004)8:5(444)
CE Database subject headings: Fiber reinforced polymers; Shape; Concrete structures; Laminates; Reinforcement; Tests.
Introduction
Advanced composite materials have been recognized as a promising repair technology for reinforced concrete or prestressed concrete structures (Nanni 2000; Balsoma et al. 2001). Common applications involve the use of externally bonded fiber reinforced polymer (FRP) laminates for both flexural and shear strengthening and confinement. The laminates are either applied with fibers parallel to the member longitudinal axis for flexural strengthening or wrapped around a member for improved shear strength (Khalifa and Nanni 2000; Khalifa et al. 2000) or confinement (Restrepo et al. 2000; Rochettee and Labossiere 2000; Monti 2001). In the case of wrapping, the need to bend the laminates over the corners of the strengthened member affects the performance and efficiency of the FRP laminate (Xiao and Wu 2000; Yang et al. 2001) to the point that the use of this upgrade technology may be limited to circular or elliptical cross sections as recommended in seismic retrofit of bridge columns (Priestley et al. 1995).
In this paper, the effect of corner radius on the performance and efficiency of carbon FRP (CFRP) laminates was investigated using a test device and method, which is relatively simple, reusable and can simulate the interaction mechanism between the FRP laminate and the substrate material. By replacing the interchangeable corner inserts in the device, member cross sections with corners having different curvature radii can be simulated. In this study, the radius of the corner inserts ranged from 0 to 50.8 mm. The test device has a symmetric configuration and the FRP laminate is wrapped around the outside surface of the device and anchored by lap splicing. The device itself puts no limitation on the number of plies to be tested and more than one ply can be installed using the procedure recommended by manufacturers for multiple laminates.
The effect of FRP wrapping on the substrate material manifests itself through the radial stress. To investigate the radial stress generated by the FRP laminate, a pressure film was installed at the interface between FRP and support material. After completion of the test, the pressure film was sent to its manufacturer for image processing. During the test, the load and strain distribution around the corner area were also recorded and the corresponding fiber stress was calculated. Finite element analysis was performed to predict the radial stress distribution and the stress distribution in the fiber direction at the curvature changing points. The finite element analysis results were compared with experimental results.
From this investigation, it was found that the structural member cross sectional shape plays an important role on the strength development of FRP wrapping. Due to the higher stress concentration, for noncircular sections with small corner radii, the strength development and the efficiency of confinement by FRP wrapping is minimum. Increasing the corner radius accordingly improves the efficiency. However, only about 70% of the ultimate strength of carbon FRP laminate can be developed even for the circular cross sections or sections with a large enough radius. The developed test device and method are viable to investigate the efficiency of FRP wrapping systems applied to cross sections with various corner radii.

Table 1. Carbon Fiber Reinforced Polymer Properties (Yang et al. 2002)
Test Program
Tensile Properties of Fiber Reinforced Polymer Material
High tensile strength carbon fiber tow sheets (MBrace 1998) were used and impregnated using a two-part epoxy polymer saturant provided by the manufacturer. Yang et al. (2002) performed tensile tests using this type of CFRP laminate, following the fabrication procedure recommended by the manufacturer, and the derived the mechanical properties are listed in Table 1. As common for manual layup fabrication, the properties revealed in the table as well as the experimental results of this project are analyzed based on the net fiber cross sectional area rather than the overall composite area. This is due to the following reasons: (1) in the manual layup technique, it is rather difficult to control the amount of resin; (2) small variations in the
amount of resin, provided that the fibers are fully impregnated, do not affect the composite mechanical performance; and (3) mechanical properties of the resin are significantly lower than those of fibers, the fibers provide virtually all of the strength and stiffness in a laminate having continuous unidirectional fibers.
Test Device
In order to simulate the force transfer mechanism of FRP wrapping a cross section through a tension test, a unique reusable test device was designed and manufactured based on the following considerations: (1) the mechanical interaction between FRP laminate and device should be similar to that of wrapped concrete members; (2) the device should be suitable for different corner radii; and (3) failure should occur in the test zone.
A general view of the entire test device is depicted in Fig. 1, which includes three independent parts, namely: corner inserts, upper part, and lower part. These three parts make a smooth and continuous outside surface on which the FRP laminate is applied. The applied load is transferred to the test device through two loading rods passing through two Φ25.4 mm holes on the upper and lower parts, respectively. A completed test device with FRP wrapping is shown later following the detailed descriptions of the three constitutive parts of the test device.
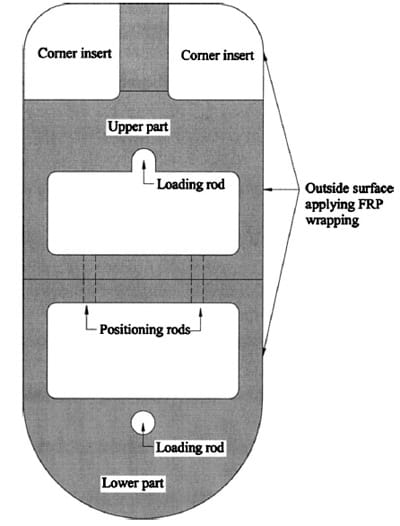
Fig. 1. General view of test device
Fig. 2(a) shows the dimensions of the upper part, combined with a pair of corner inserts. These two parts constitute the test zone, where the instrumentation is deployed and failure of FRP laminate is expected. The two interchangeable aluminum corner inserts are separated by a 51 mm wide steel block. The central block is used to help position the corner inserts and resist the load transferred from the corner inserts. The upper part has a uniform thickness of 51 mm with the overall width and height of 254 and 292.1 mm, respectively.
Fig. 2(b) shows the lower part of the test device, which is designed primarily for anchoring the FRP laminate. The semicircular bottom surface of the steel block has a radius of 127 mm under which the FRP laminate is terminated and lap spliced with a length of about 152 mm, as commonly used in practice. The radius of the semi-circular shape bottom surface is considerably larger than that of all corner inserts to guarantee better strength development and no failure is expected within the anchor zone.
Fig. 2(c) shows all of the corner inserts used in this investigation. Corner inserts are made in pairs of aluminum with any desired radius. The overall dimensions are 1023102 mm. The corner radii investigated in this investigation include: 0.00, 6.35, 12.70, 19.05, 25.40, 38.10, and 50.80 mm. The corner inserts are connected to the upper part of the test device using a conventional adhesive to prevent any movement during laminate installation and testing. Extra mechanical connections are recommended between the corner inserts and the upper part of the test device in case the impact by rupture of the FRP laminate destroys the adhesive and causes detachment of the corner inserts from the steel surface.
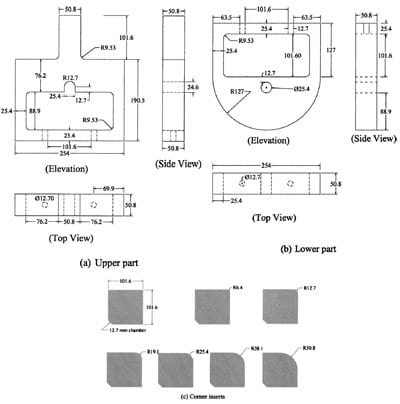
Fig. 2. Dimensions of test device (unit: mm): (a) upper part; (b) lower part; and (c) corner insets
To make a smooth and continuous outside surface for the installation of the FRP laminate, the upper and lower parts are joined and fixed using two positioning bolts. After the test device with wrapped FRP laminate is installed on the testing machine and ready for testing, the nuts on these positioning bolts are loosened so that the tensile load can be entirely transferred to the FRP laminate. The loosened bolts are kept in place during testing as a safety feature to hold the device together after rupture of the laminate.
Installation of Laminate
Upon completion of the assemblage of the test device, the FRP laminate can be installed around the outside surface. One concern exists about the interaction between the cured FRP laminate and substrate material. If the FRP laminate is bonded together with the outside surface of the test device, possible lack of uniform bonding by manual layup technique can cause nonuniform force transition in the cross section of FRP laminate and intensify the stress concentration around the corner area and stress localization. To eliminate this effect, the outside surface of the device is covered with a layer of thin but tightly applied polyethylene tape with the sticky side facing outward to contact the FRP laminate. Here, the polyethylene tape is also used as the release film to facilitate detaching of the FRP laminate from the device after completion of the test. It is to be noted that in practical confinement applications, FRP bond to the substrate is not required.
In this investigation, due to the dimension of the test device, each FRP laminate strip is 38.1 mm wide and 1.68 m long. The dimension of the FRP laminate is not a research variable because of the uniform stress distribution in the width direction of the FRP laminate. The laminate is fabricated by the manual layup procedure. First, the two-part saturant is thoroughly mixed and a thin layer is applied on both the sticky surface of polyethylene tape and the carbon fiber sheet using a sponge brush. Through careful handling, the carbon fiber ply is wrapped around the specimen starting from the top side of the test device and lap spliced at the bottom. A plastic roller is used to remove the air entrapped between fiber ply and saturant. After approximately 30 min, a second layer of saturant is applied on the fiber ply and the plastic roller is used again to work the resin into the fibers. The wet laminate is left to cure for 3 days and then strain gauges are attached. Three or more identical specimens are manufactured for each set of corner inserts in this investigation. This procedure is repeated if more than one fiber ply is applied to make the FRP laminate.
Instrumentation
Strain gauges were mounted prior to testing at multiple points to measure the strains in different locations on the FRP laminate. The first two strain gauges were placed 38.10 mm away from the root of the corner insert on the flat portion of the upper and side surfaces, respectively [see SG1 and SG4 in Fig. 3(a)]. Two other gauges are positioned with one end exactly at the curvature changing point of the upper and side surfaces [see SG2 and SG3 in Fig. 3(a)]. For those laminates with corner radius larger than 19.05 mm, a fifth strain gauge was attached at the center of the corner arc [see SG3 in Fig. 3(b)]. Strain gauges were symmetrically arranged in the corner area of both sides. Load was monitored by the built-in load cell in the testing machine.
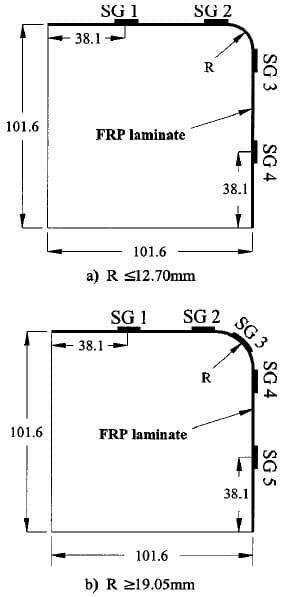
Fig. 3. Strain gauge arrangement
To measure the radial stress that the FRP laminate exerts on the surface of the substrate material, a strip of Pressurex pressure film was installed between the FRP laminate and support material right before applying the polyethylene tape. Pressurex pressure film contains a microcapsule layer with pressure-sensitive color developing agent, a color developing layer, and two protection layers. It immediately reveals the pressure distribution profile that occurs between the two surfaces when a pressure exists (SPI 2002). The color intensity of Pressurex film is directly related to the amount of pressure applied to it. The greater the pressure, the more intense the color. Conventional Pressurex pressure film can measure pressure ranging from 0.2 to 128 MPa. Also, the Pressurex film is super thin (4–8×10
-3 mm) enabling it to conform to curved surfaces, and tight spaces. A typical Pressurex film cross section is shown in Fig. 4(a).

Fig. 4. Pressure films: (a) cross section and (b) after testing
Pressure films are attached on both corners. The width of the pressure films is 10 mm and the length is dependent on the corner radius. The film should cross both curvature changing points at both corners. For each corner, two films are attached with a sensitivity range of 10–49 and 49–128 MPa, respectively, to fully capture the possible variations in radial stress. The pressure films at one corner after testing and an instrumented specimen ready for testing are shown in Figs. 4(b) and 5, respectively.

Fig. 5. Test setup
Experimental Results
Strength of Carbon Fiber Reinforced Polymer Laminates
The average ultimate load carried by CFRP laminates of three specimens for different corner radii is shown in Table 2. The individual data points of stress versus corner radius and failure modes are depicted in Fig. 6. The corresponding stress was computed using the ultimate load and the total net cross sectional area of FRP laminates at both sides of the testing device. The elastic modulus in Table 2 was obtained by dividing the average stress by the average strain. It is observed that the average ultimate load increases with corner radius for both one and two-ply laminates. The ultimate load capacity of two-ply specimens is more than twice that of the corresponding one-ply specimen with two exceptions: corner radii of 0 and 58.80 mm, which represent the square and circular section, respectively (i.e., the lower and upper bound of shape effect on the CFRP capacity in this application). It is to be noted that the stress was calculated based on net cross section area of fibers, which have a width of 38.10 mm a thickness of 0.165 mm.
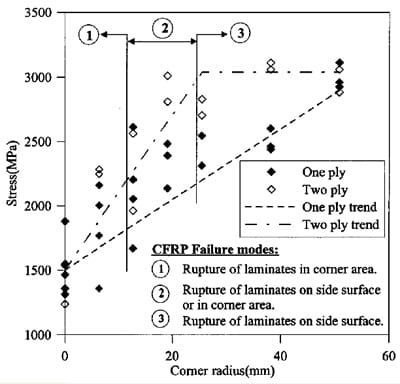
Fig. 6. Ultimate stress versus corner radius
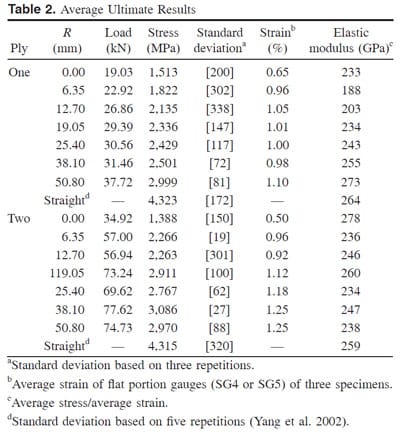
Table 2. Average Ultimate Results
Yang et al. (2002) ran tension tests and found that the average ultimate strength of this kind of CFRP laminate is 4,323 and 4,315 MPa, for one and two ply, respectively. Compared with this reference value, it can be seen that corner radius has a significant effect on the development of CFRP strength. With R=0 mm, the ultimate strength is 1,513 and 1,388 MPa for one- and two-ply laminates, respectively, which are significantly lower than the reference value. To show this effect, the average ultimate strength was normalized by the reference value (f / fu1-straight) and depicted in Fig. 7. It can be seen that only around 70% of the average unidirectional ultimate strength can be developed even for a radius of 50.8 mm for both one- and two-ply laminates. About 30% of the average unidirectional ultimate strength can be expected for cross sections with sharp corners due to the larger stress concentration and initial strain needed for bending the FRP laminate.
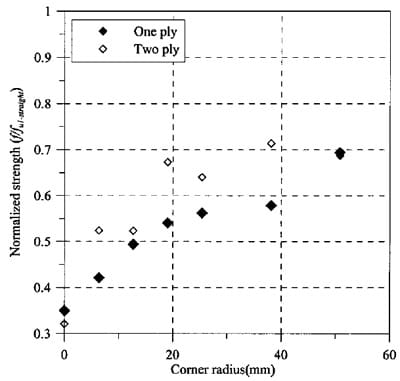
Fig. 7. Normalized ultimate stress of carbon fiber reinforced polymer laminates
Radial Stress Distribution
After completion of the tests, the pressure films were analyzed either by visually comparing the color at any location on the film with a predetermined color correlation chart or using the image process system Pointscan (SPI 2002), which offers a computerbased solution for interpreting results. This system actually converts the film’s color to a corresponding pressure level at any point on the film with a high degree of accuracy. To reduce the amount of data without losing accuracy, the films were meshed with small cells with a dimension of around 0.7 and 1.5 mm in the transverse and longitudinal direction, respectively, and an average value was obtained within each cell. Therefore a typical pressure film with a radius of 25.4 mm had at least 405 cells.
For each pressure film, only one curve was extracted by taking the average of the stresses in the thickness direction of the corner insert as indicated in Fig. 8. This is due to the fact that the stress in this direction is uniformly distributed. In the longitudinal fiber direction, in order to clearly show the ordinates and make it consistent for different corner radius, the origin is chosen in the middle of the pressure film and the angles measured from any point of the film centerline to the origin are used as the abscissa, e.g., 45 and -45° correspond to the two curvature changing points on the upper and side portion of the pressure film. Usually one corner breaks first. Fig. 8 shows the radial stress distribution of the unbroken corners for R=6.35 and 25.4 mm, data for other corner radii are presented later and compared with the theoretical results. It is noted that only the radial stress between -20 and 20° is indicated in the figure because the radial stress distribution outside this range showed more data scatter, especially for smaller corner radius. One possible reason for this scatter is the abrupt failure of the laminates, which causes significant impact around the area of curvature changing points. It is indicated that radial stress for a smaller corner radius is higher than that for a larger corner radius. However, this relatively larger radial stress for cross sections with smaller corner radius is a localized phenomenon because the confined area is a function of corner radius and the confining efficiency depends on the radial stress on the entire cross section and its distribution.
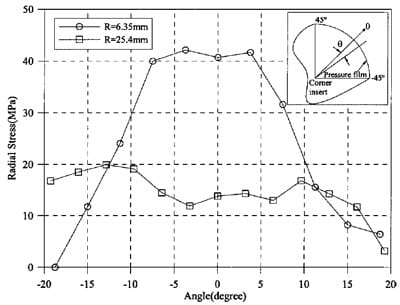
Fig. 8. Radial stress distribution
Even though different failure modes were observed at the two corners, the radial stress distribution does not show too much variation under failure load, especially for larger corner radii because immediately after the breaking of FRP laminate at one corner, the entire laminate becomes loose and detaches from the entire contacting surfaces. The supposed radial stress concentration at the curvature changing points was not identified from radial stress distribution diagrams but can be found from the pressure films where the color obviously exceeded the range of the films and was omitted by the data analysis system.
Finite Element Analysis
Analytical Model
To verify the experimental findings, finite element analysis was performed to simulate the interaction between CFRP laminate and corner insert. By taking advantage of symmetry, a quarter of the test specimen was used to construct the finite element model. The symmetric conditions were applied on the X=0 and Y =0 boundaries and a load F was applied at the end of FRP wrap at X=a and Y =0 as shown in Fig. 9. Accordingly, the displacements of all nodes in the X direction along the Y axis were constrained for both corner insert and FRP laminate elements. The displacements of all nodes in the Y direction along the X axis were constrained for corner insert only and a load F was applied to the FRP laminate. The Timoshenko beam element was adopted to simulate the CFRP laminate (Reddy 1993).
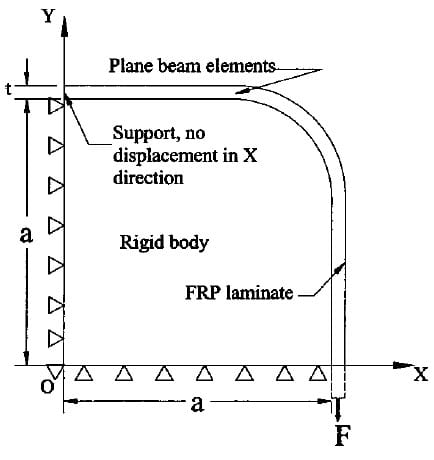
Fig. 9. Finite element analytical model
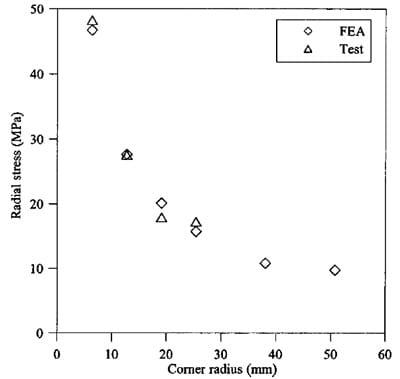
Fig. 10. Ultimate radial stress by finite element analysis and test
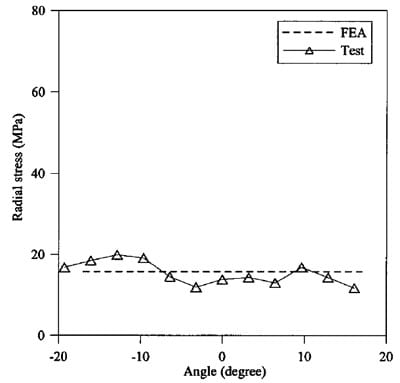
Fig. 11. Radial stress distribution in corner area for R=25.4 mm
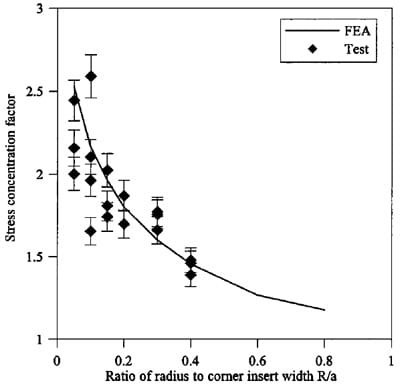
Fig. 12. Stress concentration factor
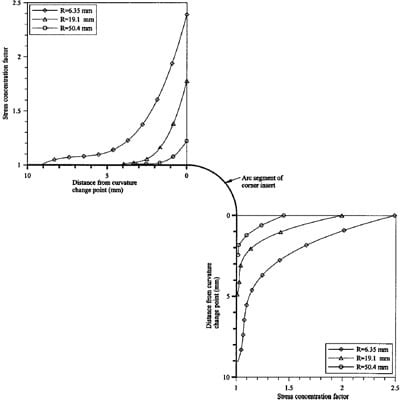
Fig. 13. Stress concentration factor distribution
A commercial finite element code, ABAQUS (1998), was used to perform the static analysis of this contact problem. The corner insert was modeled as a rigid body. Therefore, a contact interaction was modeled between the corner insert and the CFRP laminate. A finite motion along the interface between the corner insert and the CFRP laminate is allowed but no separation is tolerated between the two parts. A linear elastic material property was used for the beam elements. Two-node linear Timoshenko beam elements were used for the radius of R=6.35 mm, while three-node quadratic Timoshenko beam elements were used for the calculations of all other radii. The length of the two-node linear beam elements in the curved segment is 0.166 mm, while the length of three-node quadratic beam elements in the curved segment changes from 0.665 to 1.0 mm depending on the radius of the corner insert. The Young’s modulus of FRP laminates is 264 GPa (Yang et al. 2002). It should be noted that the finite element analysis (FEA) was conducted only for one-ply CFRP laminates for the stress profile under different load levels.
Results and Discussion
Fig. 10 shows the FEA and experimental results of ultimate radial stress versus radii of the corner inserts. It is shown from the figure that there is a good agreement between the FEA and average test measurements. The ultimate radial stress decreases with increasing the corner radius in a nonlinear manner. Fig. 11 shows the radial stress distribution at the arc segment of the corner insert from both FEA and experimental results for R=25.4 mm. It is to be noted that, in FEA, the arc segment has a constant radius and curvature generating a constant value of radial stress.
It can be seen from Fig. 9 that the curvature radius changes from infinity in the straight portion of the corner insert to a finite value 1/R in the arc segment of the insert which means that stress concentration will occur at these points in the CFRP laminate. The stress concentration factor versus ratio of radius of the corner insert to its width sR/ad is shown in Fig. 12 for both FEA and experimental results. The definition of corner insert width is shown in Fig. 9. In FEA, the stress concentration factor is defined as the ratio of the maximum fiber stress at the curvature changing point to that at the load application point. For the test results, they were obtained by using the reference strength 4,323 MPa divided by the individual ultimate stress of CFRP laminate for different corner radii. It is observed in the figure that the FEA results agree well with experimental results. When the radius of the corner insert decreases, the factor increases sharply. Fig. 13 shows the stress concentration factor distributions near the curvature changing points between the straight and arc segment for three typical cases with R=6.35, 19.1, and 50.8 mm, respectively. It is shown that the smaller the corner radius, the more severe the stress concentration.
Conclusions
Based on the investigations of both experiments and numerical analyses, the following conclusions can be reached:
- The testing method and the reusable test device are reliable for investigating the effect of corner radius on the performance of FRP laminates when wrapping structural cross sections.
- A smaller corner radius can significantly reduce the ultimate strength of the FRP laminate due to stress concentration around the corner area. The stress concentration factor increases when the corner radius decreases.
- Radial stress on FRP lmainate relates with corner radius in a different way, it decreases with increasing corner radius.
- The finite element method can predict the stress concentration in the fiber direction and the radial stress distribution.
- The numerical results agree well with the experimental ones.
- Additional research is necessary on the measurement of radial stress and radial stress distribution for different types of FRP material systems and geometries.
Acknowledgment
Financial support from the Federal Highway Administration (FHWA) under Contract No. DTFH 61-00X-00017 is greatly appreciated.
References
- ABAQUS/standard user’s manual, Version 5.8. (1998). Hibbitt, Karlsson & Sorenson, Inc. Pawtucket, R.I.
- Balsoma, A., Coppola, L., and Zaffaroni, P. (2001). “FRP in construction: Applications, advantages, barriers, and perspectives.” Proc., Int. Workshop: Composites in Construction, A. Reality, E. Cosenza, G. Manfred, and A. Nanni, eds., Capri, Italy, 58–64.
- Khalifa, A., and Nanni, A. (2000). “Improving shear capacity of existing RC T-section beams using CFRP composites.” Cem. Concr. Compos., 22(2), 165–174.
- Khalifa, A., De Lorenzis, L., and Nanni, A. (2000). “FRP composites for shear strengthneing of RC beams.” Proc., 3rd Int. Conf. on Advanced Composites Materials in Bridges and Structures, J. Humar, and A. G. Razaqpur, eds. Ottawa, 137–144.
- MBrace. (1998). Composite strengthening system, engineering design guideline, 2nd Ed., Master Builders Technologies, Inc., Cleveland.
- Monti, G., (2001). “Confining reinforced concrete with FRP: Behavior and modeling.” Proc., Int. Workshop: Composites in Construction, A. Reality, E. Cosenza, G. Manfred, and A. Nanni, eds., Capri, Italy, 213–222.
- Nanni, A., (2000). “Carbon fibers in civil structures: Rehabilitation and new construction.” Proc., Global Outlook for Carbon Fiber 2000, Intertech, San Antonio.
- Priestley, M. J. N., Seible, F., and Calvi, M. (1995). Seismic design and retrofit of bridges, Wiley, New York.
- Reddy, J. N. (1993). An introduction to the finite element method, 2nd Ed., McGraw-Hill, Boston.
- Restrepo, J. I., Wang, Y. C., Wymer, P. A., and Irwin, R. W., (2000). “Recent developments in the use of advanced composite materials for seismic retrofitting.” Proc., 12th World Conf. on Earthquake Engineering, Auckland, New Zealand, (CD-ROM).
- Rochette, P., and Labossiere P. (2000). “Axial testing of rectangular column models confined with composites.” J. Compos. Constr., 4(3), 129–136.
- Sensor Products Inc. (SPI). (2002). “Pressurex tactile pressure film specifications.” East Hanover, N.J.
- Xiao, Y., and Wu, H. (2000). “Compressive behavior of concrete confined by carbon fiber composite jackets.” J. Mater. Civ. Eng., 12(2), 139– 146.
- Yang, X. B., Nanni, A., and Chen, G. D. (2001). “Effect of corner radius on the performance of externally bonded FRP reinforcement.” Proc. 5th Int. Conf. on Non-Metallic Reinforcement for Concrete Structures, (CD-ROM), Cambridge, U.K.
- Yang, X. B., Nanni, A., Haug, S., and Sun, C. L. (2002). “Strength and modulus degradat
ion of carbon fiber-reinforced polymer laminates from fiber misalignment.” J. Mater. Civ. Eng., 14(4), 320–326.


