M. Costanzi**, V. Rouillard*, D. Cebon**
**Engineering Department, University of Cambridge, England
*School of Architectural, Civil and Mechanical Engineering, Victoria University,
Melbourne, Australia
Presenter: M. Costanzi
Research Student
Engineering Dept., Trumpington St., Cambridge, England
+44 01223 766320
[email protected]
ABSTRACT
This paper present the preliminary findings of research aimed at determining the character of the contact pressure distribution of crane tyres and estimating their influence on the deformation of pavements. The impetus for the research was: (i) the requirement of the (Australian) regulation for a minimum tyre size of 20.5-inch (525mm) for all-terrain cranes with a maximum allowable axle load of 12 tonnes; and (ii) the Australian crane industry’s argument for the adoption of smaller tyres with reduced inflation pressures based on the expectation of increased contact area, hence reduced contact pressure. The paper describes the use of pressure-sensitive film to generate a digital field proportional to contact pressure. The results show that the contact pressure distributions measured were complex and not uniformly-distributed over a circular area as is assumed in conventional pavement analysis. The pressure distribution maps revealed large localised contact pressures (often greater that three times the mean net contact pressure) at the edge of individual tread blocks. The measured data were used to study the effects of realistic contact pressure distributions on the deformation rates of flexible pavements, using Finite Element Analysis based on a non-linear visco-plastic strain and temperature dependent constitutive model.
1. INTRODUCTION
Most pavement analysts have assumed that the normal component of the contact pressure between tyre and road surface is uniform, acts over a circular area and is nominally equal to the inflation pressure (see, for example [1-3]). It has been widely acknowledged [4, 5] that these assumptions are over-simplistic and that contact patch area, shape and pressure distribution vary significantly depending on tyre type, tread pattern, inflation pressure and load. It has also been shown [6] that the simplifications lead to an underestimation of pavement stresses. The localised peaks in the pressure distribution have been shown to result in increased overall rutting.
Under normal inflation and loading conditions, the maximum shoulder pressure is observed to be twice the inflation pressure [7-9], although the contact pressure distribution is found to be more uniform for higher inflation pressures and/or lower vertical loads [8, 9].
A number of authors have calculated [2, 7, 10], or measured [10-13], the influence of tyre contact conditions on stresses and strains in the road surface. The general consensus is clear: the details of the contact conditions, such as the exact area, pressure and pressure distribution, affect stresses and strains near to the surface of the pavement, whereas the response in the lower layers depends mainly on the overall load [2, 7, 10, 14].
Roberts et al [7] and Marshek et al [15] applied non-uniform, axisymmetric contact pressure distributions to elastic layer pavement models. Both studies established that assumptions about contact conditions can alter predicted horizontal strains at the bottom of thin surface layers (less than 50 mm) substantially, particularly for under-inflated tyres which have large shoulder contact pressures. The effects of non-uniform loading are much less significant for vertical compressive subgrade strains and for thicker pavements.
Research into pavement damage confirms the localised influence of contact conditions [6, 14]. Roberts et al [7] and Haas and Papagiannakis [2] estimated rut formation by summing theoretical permanent deformations of the pavement layers and both ascertained that rutting damage is sensitive to contact pressure. Laboratory measurements by Eisenmann et al [10] on a 225 mm thick asphalt road surface model showed that rut depth development was approximately linearly related to the average contact pressure, (independent of load).
The aim of the research in this paper is to investigate the effects of tyre contact pressure distribution on surface deformation. It has two new features compared to previous work: (i) It uses uniquely detailed measurements of tyre contact pressures generated by heavy vehicle tyres; (ii) it utilizes a new nonlinear, visco-plastic model of asphalt deformation, based on recent materials research, and implemented using finite element analysis.
2. TYRE CONTACT PRESSURE MEASUREMENTS
Vertical contact pressures were measured with pressure sensitive film, Pressurex®. Pressurex is a Mylar film containing a layer of dye – filled microcapsules which, upon application of force, rupture producing an immediate and permanent high-resolution topographical image of pressure variation across the contact area. Although the maximum rated pressure of the film used was specified at 2.5 MPa, calibration, undertaken at various environmental conditions, revealed a significantly larger dynamic range (Figure 1)
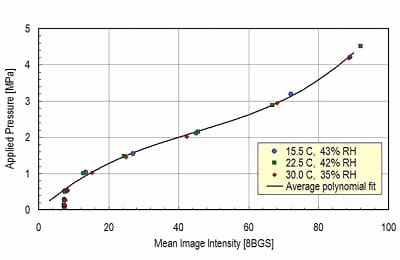
Figure 1 – Calibration data for pressure sensitive film – 5 seconds exposure

Figure 2 – Photographs of measurement set up.
The distribution of contact pressure normal to the pavement surface was measured by slowly lowering one wheel of a loaded crane (adjusted to 6 tonnes per wheel) onto a sheet of pressure sensitive film placed between the tyre and a wheel scale as shown in Figure 2. The load was maintained for 5 seconds before being removed by activating the crane’s stabiliser jacks. This was done for various tyre inflation pressures.
Each imprint, eg Figure 3(a), was scanned at 200 dpi with an optical scanner using an 8 bit, grey scale, bit-map format for computer analysis. This included application of a Gaussian blur algorithm to smooth-out the data and minimise the effects of localised pressure variations (noise) produced by the very high spatial resolution of the film as shown in Figure 3(b).
The image was calibrated (using Figure 1) and the result was a contour map of the pressure distribution as per Figure 4. A section through such a contour map gives the pressure distribution along a line through the contact patch, see, for example, Figure 5.
It can be seen that the pressures at the edges of each tread block can be more than double the pressure in the middle of the block.

Figure 3 – (a) Example of an imprint from the pressure sensitive film; (b) effect of a 3.2mm Gaussian blur filter on digitised an 8BGS image.
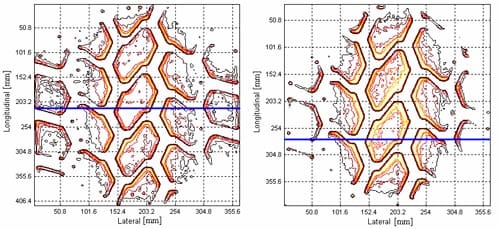
Figure 4 – Examples of pressure distributions from scanned picture of the imprint for a Michelin XGC 1600 R25 tyre, width 16”. (a): inflation pressure 6 bar, (b): inflation pressure 9 bar.
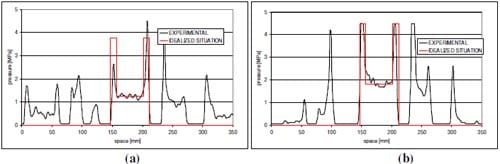
Figure 5 – Transverse sections of the pressure distribution across the contact patch of a Michelin XGC 1600 R25 tyre, width 16″, along the blue lines in Figure 4. (a) inflation pressure 6 bar, (b) inflation pressure 9 bar
3. ASPHALT DEFORMATION MODEL
The mechanical behaviour of asphalt mixtures depends on the quantity, size, shape, grading and properties of the aggregate, the behaviour of the bituminous binder and the presence of additives [16].
Based on the work of Cheung [17] and Deshpande [18, 19], Ossa [20] showed that the transient triaxial deformation behaviour of bitumen can be expressed using an extended version of the ‘Modified Cross Model’, given by:
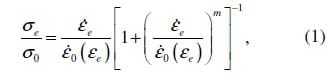
where the equivalent stress and strain are given (in tensor notation) by ![]()
![]() . Ossa demonstrated that the experimental parameters ε0c(ε), δ0, m and k can be measured to reasonable accuracy with a minimum of four ordinary compressive or tensile tests [20].
. Ossa demonstrated that the experimental parameters ε0c(ε), δ0, m and k can be measured to reasonable accuracy with a minimum of four ordinary compressive or tensile tests [20].
The reference strain-rate ‘master curve’ ε0c(ε), which is a function of strain ε, can be measured in a creep test at a constant stress δ0 at the absolute temperature Tref. At any other absolute temperature ref T ≠ Tref the reference strain rate is given by:
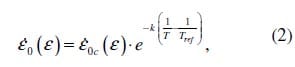
where k is the Arrhenius experimental constant.
Note that if εe/ε0 << (small strain-rate), equation (1) reverts to linear viscous behaviour:
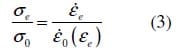
Desphande and Cebon [18, 19] found that adding aggregate to bitumen has two main effects on the mechanical behaviour of the material:
- Under a uniaxial (compressive) stress field, the aggregate strengthens the bitumen by a constant factor, independent of strain rate and temperature.
- Under triaxial stress conditions, high volume fractions of aggregate generate dilation in the mix when it is subjected to deviatoric stresses. Since the dilation acts against any applied hydrostatic stresses, the effect is pressure sensitivity. Consequently, like soils, asphalt mixes effectively strengthen as the hydrostatic pressure increases.
Ossa [21] showed that the deformation model for bitumen can be extended to asphalts by introducing a strengthening function q(η), which is the ratio of the steady-state strain rate of a specimen of asphalt to the steady-state strain rate in a specimen made of pure bitumen. It is a function of the stress ratio η:

Then equation (1) can be written:
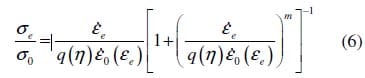
In the parametric study that follows a model of pure bitumen (equation 1) is used as a first attempt to understand the effects of the material nonlinearity on surface deformation. Since the constitutive laws for bitumen and asphalt have exactly the same form for the case of zero hydrostatic pressure, the relative effects of the parameters elucidated with the bitumen model are expected to be similar for asphalt mixes. A finite-element model of the deformation behaviour of asphalt is currently under development and will be used to obtain a more accurate understanding of the influence of aggregate dilation (parameter q(η) in equation (6) )on the deformation response.
The model described in equation (1) was applied to a 50 penetration grade pure bitumen. It was calibrated as per [20], using a dumbbell specimen like the one in Figure 6. The results of calibration were the master curve for ε0c(ε) in Figure 7.
A material deformation model, suitable for finite element analysis, was created for pure bitumen, according to equation (1), using the ABAQUS FEA programme. This subroutine was validated against experimental result from tensile tests on dumbbell bitumen specimens. The agreement of experiments, FEA and analytical solution was found to be good, as shown in Figures 8 and 9.
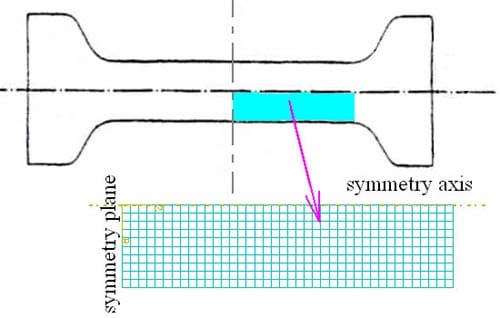
Figure 6 – Dumbbell specimen used in the characterization of bitumen. The central gage section is 80 mm long and 20 mm in diameter. In light blue the section of the axi-symmetric model used in FEA simulations.
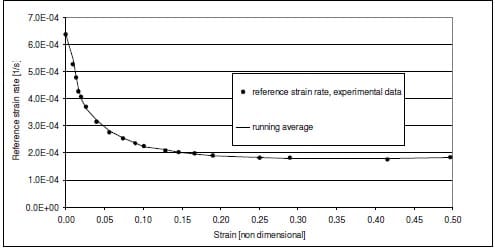
Figure 7 – Master curve for a 50 pen bitumen at 273K (from experiments performed by Ossa [20]). Penetration grade = 53 dmm; Softening point = 53.5°C; k=22.8 103 K; m=0.615; δ0 = 0.2 MPa
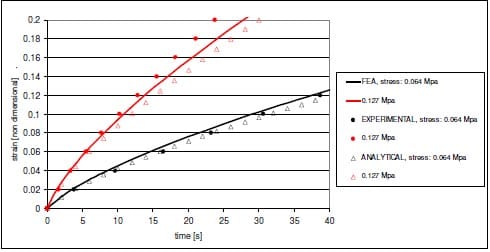
Figure 8 – Constant stress tensile tests on a dumbbell specimen made from 50 pen bitumen at 283K. Comparison between esperimental results [20], FEA results and analytical solution.
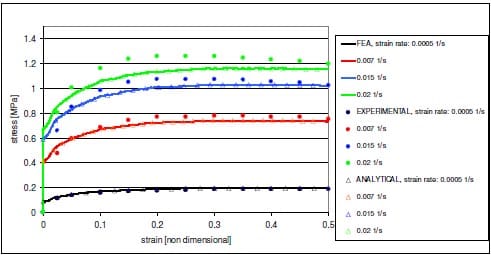
Figure 9 – Constant strain-rate tensile tests on a dumbbell specimen made from 50 pen bitumen at 273K. Comparison between experimental results [20], FEA results and analytical solution.
PARAMETRIC STUDY
It is evident from Figure 4, that the pressure in the contact patch is a function of the inflation pressure. When inflation pressure is higher, the contact patch becomes smaller and more rounded, and the average contact pressure increases. It is also evident that each tread lug has a significantly higher pressure all around its perimeter than its interior. In Figure 5 the pressure distribution in the most highly stressed lug was idealized by a symmetric distribution (in red) with a flat middle area and peaks at either side. The width of the lug in this particular in this cross section is about 65 mm.
A parametric study was performed, simulating the effect of the contact pressure distribution of one lug, using an axi-symmetric FE model (see Figure 10), with the bitumen creep model described above. The pressure field was approximated by a central circular area Scentr with a uniform pressure pcentr, surrounded by a concentric perimeter ring with area
Sper and uniform pressure pper . The shape of the pressure field is completely described by two nondimensional parameters:
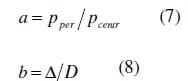
where D is the diameter and Δ is the width of the outer perimeter region of the tread element (figure 10).
The values of parameters a and b were varied within likely practical limits: a was varied from 0 to 3. (a=0 corresponds to a uniform pressure distribution, while in experimental measurements it was observed to vary in the range a=2 to a=3.) Parameter b was varied between 0 and 0.23. (In the experiments b = 0.1). The outer diameter was D = 65mm in all simulations. The load was ramped from zero to the nominal value in 1 sec, then kept constant for an additional 19 sec.
Deformation profiles at the end of the 20s of loading, for an average pressure of 1.8 MPa are given in Figure 11. It can be seen that concentrating the load in the centre of the tread element significantly increases the deformation.
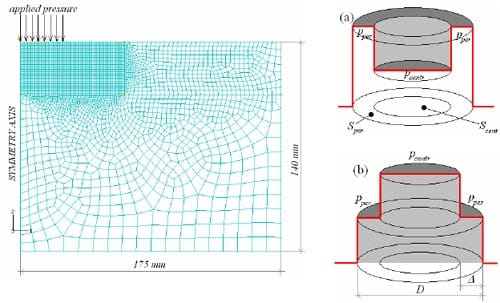
Figure 10 – The axi – symmetric model used for FEA. Elements are linear full integration, axisymmetric in the area of maximum mesh refinement (approx. 1×1 mm) and linear reduced integration, axisymmetric elsewhere. Two examples of the pressure distribution are shown on the right: (a): a > 1, (b): a < 1
Figure 12 quantifies the volumetric displacement rates obtained for a = 0 (a uniform pressure distribution), as a function of parameter b, for two different material models: the nonlinear model of 50pen bitumen, as per equation (1) with m = 0.615, and a simplified linear viscous model in which parameter m in is set to 0. For small b, the contact area is large and the pressure is correspondingly small. For large b the contact area is small and the pressure is large.
For the linear viscous case, the volumetric displacement rate is practically insensitive to the value of b (hence the value of pcentr). This is a direct consequence of the linear viscous model. The overall volumetric displacement rate in the vicinity of the lug is only a function of the total force on the lug. If the area increases, the pressure and hence local displacement rate decrease proportionately (to keep the same load) so that the product of area and displacement rate remains constant. This is far from true for the nonlinear model. In this case, the effect of the power m is to amplify the deformation due to high stresses so that the deformation rate increases dramatically for high values of b.
Figure 13 shows the volumetric displacement rates as a function of a for several values of b. The red icons indicate the wide range of pressure profiles considered. The volumetric displacement rate is normalized with respect to the case where b = 0 (uniform pressure). It can be seen that for the range of parameters a and b considered, the high shoulder pressures have little effect on the overall deformation rate for large values of a. Conversely, decreasing the overall contact area and increasing the contact pressure over the central area (small values of a) substantially increases the volumetric deformation rate.
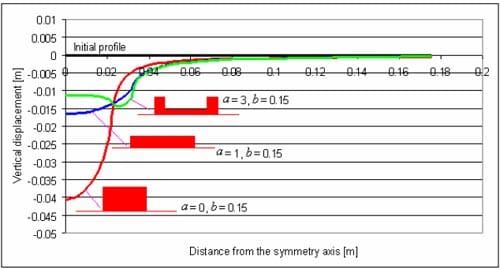
Figure 11 – Examples of results of FEA simulations (final time: 20 sec) on the effect of various pressure distributions on a 50 pen bitumen half space at 0°C. Average contact pressure 1.8MPa. The red icons show the pressure distribution to scale.
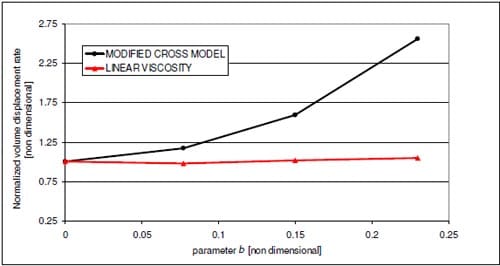
Figure 12 – Results of FEA simulations on the effect of various pressure distributions with a = 0 on a 50 pen bitumen half space only at 0°C. Average contact pressure 1.8MPa.
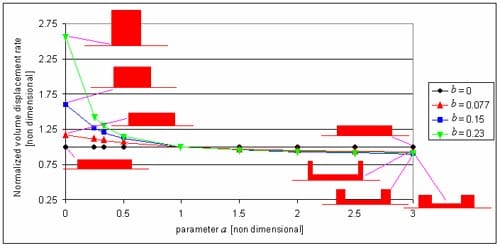
Figure 13 – Results of FEA simulations on the effect of various pressure distributions on a 50 pen bitumen half space at 0°C. Average contact pressure 1.8MPa. The red icons show a section through the pressure distribution.
CONCLUSIONS
- The pressure field under a stationary tyre can be measured simply and reliably using a pressure sensitive film. The system has been demonstrated on a crane tyre but it can be extended on any type of tyre.
- The pressure field under a tyre shows a complex large-scale distribution that depends on the applied load and the inflation pressure, and a small-scale distribution due to individual tread elements. The pressure sensitive film can measure both. It is clear that idealising the crane tyre as a circular contact patch with a uniform contact pressure distribution is very inaccurate.
- The non-linear ‘modified cross model’ (MCM) was implemented in a finite element code and demonstrated to be accurate for modelling the behaviour of pure bitumen in tension. It is thought that the broad results should extend to models of asphalt pavement surfaces, although with much lower deformation rates. Note however that the effect of dilation of the aggregate may cause an effect of interaction between adjacent tread blocks. This is the subject of on-going research.
- The FEA simulations of the effect of pressure on deformation of a bitumen pavement show that the small-scale peaks at the edge of the tyre lugs have little effect on the overall pavement deformation for the range of parameters considered. Conversely, the overall contact area and pressure have a significant effect on deformation because of the nonlinearity of material response.
REFERENCES
- DeBeer, M. and C. Fisher, Contact stresses of pneumatic tyres measured with the vehicleroad surface pressure transducer array. 1997, CSIR: Pretoria, South Africa
- Haas, R.C.G. and A.T. Papagiannakis. Understanding pavement rutting. in Special workshop on rutting in asphalt pavements. 1986. Toronto: Roads and Transport Association of Canada.
- Brown, S.F., A.F. Stock, and P.S. Pell, The structural design of asphalt pavements by computer. The Highway Engineer, 1980. 27(2-10).
- DePont, J., The impact of small diameter tyres on pavement wear. 2000, Transfund New Zealand
- Anon, National Crane Review Project. 2000, National Road Transport Commission, Australia, Estill & Associates Pty Ltd
- Weissman, S.L., Influence of tyre-pavement contact stress distribution on development of stress mechanisms in pavements. Transport Research Record, 1999. 1655(99-0774): p. 161-167.
- Roberts, F.L., et al., Effects of tire pressures on flexible pavements. 1986, Texas Transportation Institute Research. p. 245
- Tielking, J.T. Finite element tire model. in FHWA Load Equivalence Workshop. 1988. Washington D.C.
- Yap, P. A comparative study of the effects of truck tire types on road contact pressures. in SAE Conference on Vehicle/Pavement Interaction, SAE SP765, SAE Trans. 881847. 1988. Indianapolis.
- Eisenmann, J., D. Birman, and A. Hilmer, Effects of commercial vehicle design on road stress – research results relating to the roads. Strasse und Autobahn, (Translated by TRRL as WP/V&ED/87/29), 1987. 37(6): p. 238-244.
- Christison, J.T., K.O. Anderson, and B.P. Shields, In situ measurements of strains and deflections in a full-depth asphaltic concrete pavement. Proc. Assoc. Asphalt Paving Technology, 1978. 47: p. 398-430.
- Zube, E. and R. Forsyth, An investigation of the destructive effect of floatation tires on flexible pavement. Highway Res. Rec., HRB, 1965. N71: p. 129-150.
- Addis, R.R. The effect of wheel loads on road pavements. in IMechE conference on road wear: The interaction between vehicle suspensions and the road. 1991. London.
- Chan, G.P., et al. Laboratory measured tire-pavement contact pressures. in FHWA Load Equivalence Workshop. 1988. Washington D.C.: FHWA.
- Marshek, K.M., et al., Effect of truck tire inflation pressure and axle load on flexible and rigid pavement performance. Transp. Res. Rec. TRB, 1986. 1070: p. 14-21.
- Deshpande, V.S. and D. Cebon, Micro-mechanical modelling of steady-state deformation in asphalt. Journal of Materials in Civil Engineering, 2004. 16(2).
- Cheung, C.Y. and D. Cebon, Deformation mechanisms of pure bitumen. ASCE Journal of Materials in Civil Engineering, 1997. 9(3): p. 117-129.
- Deshpande, V.S. and D. Cebon, Steady-state constitutive relationship for idealised asphalt mixes. Mechanics of Materials, 1999. 31: p. 271–287.
- Deshpande, V.S. and D. Cebon, Uniaxial experiments on idealised asphalt mixes. Journal of Materials in Civil Engineering, 2000. 12(3): p. 262-271.
- Ossa, E.A., V.S. Deshpande, and D. Cebon, Phenomenological model for the monotonic and cyclic behaviour of pure bitumen. Journal of Materials in Civil Engineering, 2005. 17(2): p. 188-197.
- Ossa, E.A., V.S. Deshpande, and D. Cebon, Triaxial deformation behaviour of bituminous mixes. Submitted to J. Materials in Civil Engineering, 2006.


