Susanna Pirttikangas, Jaakko Suutala, Jukka Riekki and Juha Roning
Intelligent Systems Group, Infotech Oulu
FIN-90014 University of Oulu
[email protected]
Abstract
This paper reports initial experiments on recognizingwalkers from measurements with a pressure-sensitive floor, more specifically, a floor covered with EMFi material. A 100 square meter pressure-sensitive floor (EMFi floor) was recently installed in the Intelligent Systems Group’s research laboratory at the University of Oulu as part of a smart living room. The floor senses the changes in the pressure against its surface and produces voltage signals of the event. The test set for footstep identification includes EMFi data from 3 walkers. The testees walked casually around the floor for 30 seconds, and the steps were extracted from the data and featurized. Identification was made with discrete Hidden Markov Models. Although the research is preliminary, the results show a 78 % overall success rate of footstep identification and are hence very promising.
1. Introduction
The research on intelligent environments [1], [2], [3] aims at making smart houses, offices, tourist attractions etc., where the environment learns and reacts to the behaviour of the occupants. The methodology can be applied in homes for the elderly and disabled as an enabling technology for monitoring hazardous situtations as well as in surveillance systems or in child care. Automatic recognition of the occupants without a need for wearable sensors leads to personal profiling and enables smooth interaction between the environment and the occupant.
In this paper, initial experiments on recognizing walkers on a pressure-sensitive floor are described. In this initial phase, discrete Hidden Markov Models were used in the identification. The EMFi material installed under the laboratory floor during the building stage was used in making the measurements.
The idea of using footsteps to identify persons is not new. Hidden Markov Models and Nearest-Neighbor classification have been used in recognizing walkers and applied in [4] and [5], respectively. The difference compared to our research is the utilization of dissimilar sensors that measure the vertical component of the ground reaction force caused by the weight and inertial forces of the body. Furthermore, the other studies have had only small areas covered with sensors throughout the floor which is capable of measuring the steps, while we have the whole floor area cabable of measurement.
In the next section, the EMFi material and the layout of the testing area are introduced. In section 3, the basic characteristics of Hidden Markov Models are presented. The data set collected and the preprocessing are described in section 4. The test results are presented in section 5. Finally, some conclusions are drawn and future work is clarified.

Figure 1. The setting for EMFi sensor stripes under the laboratory’s normal flooring.
2. EMFI Material
ElectroMechanical Film [6] (EMFi) is a thin, flexible, lowprice electret material, which consists of cellular, biaxially oriented polypropylene film coated with metal electrodes. In the EMFi manufacturing process, a special voided internal structure is created in the polypropylene layer, which makes it possible to store a large permanent charge in the film by the corona method, using electric fields that exceed the dielectric strength of EMFi. An external force affecting the EMFi surface causes a change in the film’s thickness, resulting in a change in the charge between the conductive metal layers. This charge can then be detected as a voltage. EMFi is a Finnish innovation and a trademark of EMFiTech Ltd.
EMFi material has been used for many commercial applications, such as keyboards, microphones in stringed musical instruments and small and large area sensors. A Finnish company, Screentec Ltd, has developed vandalproof keyboards and keypads using EMFi foil protected by a steel or plastic plate. EMF Acoustics Ltd has produced EMFi-based microphones for different stringed instruments, such as bass guitars, acoustic guitars and violins.
EMFi material has been installed in the Intelligent Systems Group’s (ISG) research laboratory at the University of Oulu. The covered area is 100 square meters. The EMFi floor in the ISG laboratory is constructed of 30 vertical and 34 horizontal EMFi sensor stripes, 30 cm wide each, that are placed under the normal flooring (see Figure 1). The stripes make up a 30×34 matrix with a cell size of 30×30 cm. Instead of simply installing squares of EMFi material under the flooring, stripes were used, because this layout requires clearly less wiring. If squares were installed, the number of wires would be over a thousand. If a smaller room were to be covered with EMFi material, squares could be used. This would make it easier to determine the locations of the occupants in the room.
Each of the 64 stripes produces a continuous signal that is sampled at a rate of 100Hz and streamed into a PC, from where the data can be analyzed in order to detect and recognize the pressure events, such as footsteps, affecting the floor. The analogous signal is processed with a National Instruments AD card, PCI-6033E, which contains an amplifier. It would be possible to increase the sampling frequency up to 1.56 kHz, but 100Hz was considered adequate for this application.
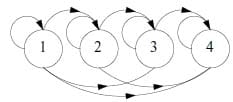
Figure 2. A 4-state left-right HMM.
3. Hidden Markov Model Classification
Hidden Markov Models (HMM) provide a natural way for modelling time-dependent signals, and they have been widely used for speech recognition [7]. Other applications concern context recognition [8] and robotics [9], for example. Here, the theory of Hidden Markov Models is described briefly, but a more extensive introduction can be found in [10].
In HMM-based classification, it is assumed that the observation sequence Θ = Θ1Θ2…ΘT(to be classified) is generated by a Markov model. A Markov model is a finite-state machine, which changes its state once every time unit. Each time t a state Sj is entered, a vector Θt is generated from a certain probability distribution B. The transition probabilities between the states and the output probabilities determine the joint probability that Θ is generated by the model. In practice, only the observation sequence is known, while the underlying state sequence is hidden, which is why they are called Hidden Markov Models.
T
here are different types of HMMs specified by the possible connections between states. In an ergodic (fully connected) HMM, every state of the model can be reached from every other state. In many speech recognition applications, the left-right model [11], [12], depicted in Figure 2, is used. In a left-right HMM, the state index increases or remains unchanged as time increases. This property leads to a natural choice of left-right models for modelling signals that change over time. Left-right HMMs are also used in this paper.
Thus, a HMM is a probabilistic model and it can be fully described by two model parameters (N and M), specification of observation symbols and three probability measures, A, B, and ϖ. Generally, the notation λ = (A,B,ϖ) is used for a HMM. It should be noted that if the modelled parameters are continuous, the observation distribution B within the HMM is continuous. In this paper, discrete HMMs are used. Therefore, the observation symbol density distribution B is discrete.
The model parameter N refers to the number of states in the model; S = {S1,S2,…,Sn}. The number of distinct observation symbols per state is M. This discrete alphabet corresponds to the output of the system being modeled. The alphabet can be generated by forming a codebook with Learning Vector Quantization [13], for example.
The probability distribution A = {aij} is the state transition probability distribution

Therefore, the state sequence is determined to start in state 1. In the classification, one HMM is assigned for each class, based on examples. Given an observation sequence Θ = Θ1Θ2…ΘT, the parameters λ = (A,B,ϖ) are determined to maximize P(Θ|λ) This can be done via Baum-Welch estimation [14] (equal to the EM method [15]) or by using gradient methods [7]. Here, Baum-Welch estimation is used.
The observation sequence is obtained from the signals via a codebook. The signals to be classified are featurized, and the prototype vector that is nearest (in some optimal sense) is assigned to the feature vector from the codebook. The index of the prototype vector is the input for the discrete HMM.
In determining the model’s distributions, it is essential to be able to choose an optimal state sequence Q = q1q2…qt corresponding to the given observation sequence. In Baum-Welch estimation, the model parameters are given initial values, and a maximum likelihood state sequence is calculated (via the Viterbi algorithm [16], for example) and it is used to improve the initial values. This process is repeated until the estimated parameters for the model do not change. The details of Baum-Welch estimation ar e beyond the scope of this paper.
In applying the models to classification, the probability of the observation sequence Θ given the model, that is, P(Θ|λ) is calculated. This likelihood determines the model from which the observation most likely came.
In Figure 3, footstep identification with HMMs is shown. First, the observation sequences acquired from each person’s steps are used for training the three models M1, M2 and M3. Then, the unknown observation sequence is identified by defining the maximum likelihood for each model.
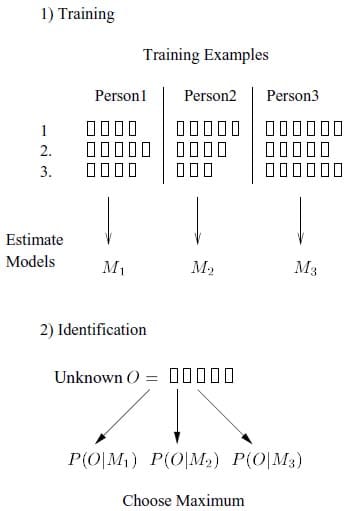
Figure 3. Using HMMs for walker identification
In this work, the HTK Toolkit version 3.2 [17] developed at the Speech Vision and Robotics Group of the Cambridge University Engineering Department, was used for creating the codebook and the Hidden Markov Models.
4. DATA
The data were collected in the autumn 2002 and consist of the measurements of 3 persons walking casually on the pressure-sensitive floor. Each person walked alone around the room for 30 seconds. The setting was made as natural as possible. All the testees weighed 66 kg + 2 and wore shoes.
During the test, all of the 64 EMFi stripes produce noisy data (see Figure 4, which shows the data recorded from one channel during the test). The footsteps must be identified and segmentated from noisy channel data. The segmentation problem is being studied in a different project. The amplitude of a step is very large compared to signal noise variance, and no filtering of the noise is therefore needed
Different problems arise in finding “good-quality” steps for modelling. If a person steps on the crossing of two stripes (see Figure 4; the last peak in the voltage signal), the amplitude of the step is lower than if he stepped on the centre of one stripe. This is natural, because only a small part of the step hits on the particular stripe. Furthermore, the amplitudes of steps in the neighborhood of the actual measurement device are higher than those further away.

Figure 4. Raw EMFi data from one stripe. The x-axis represents time in seconds and the y-axis voltage.
The problems mentioned earlier affect the selection of the signal segmentation algorithm. In this initial phase, raw segmentation was made with hybrid-median filters [18], and the best footsteps were selected manually. The data from three persons’ extracted footsteps are shown in figure 5.
The data set was divided into a training set and a test set in such a way that 50 % of the footsteps were used in training the Hidden Markov Models for each person, and the rest were used for testing the models.
The observation sequences from footsteps were aquired using a window of width N and overlapping M, as in [4]. Different window widths and overlapping segments were tested. The features obtained from each window were the mean, standard deviation, minimum and maximum of the amplitude of the pressure signal. A codebook for these observation sequences was formed with learning vector quantization. Differents numbers of states and codebook sizes were tested as well.
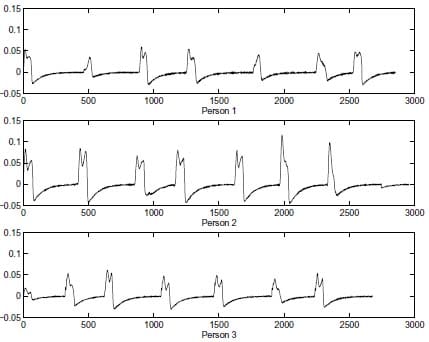
Figure 5. The extracted footsteps of three persons.
5. Test Results
The best initial results were obtained with a window width of 15 and overlapping of 5. The number of nodes in the HMM in this case was 6. The results are presented in Table 1.
| Person1 | Person2 | Person3 | |
| Person1 | 72.20 | 27.80 | 0.00 |
| Person2 | 36.84 | 63.16 | 0.00 |
| Person3 | 0.00 | 4.80 | 95.2 |
Table 1. Confusion matrix for three persons’ footsteps.
It can be seen that the footsteps of person number 3, are most distinguishable. There is notable confusion in the footsteps of the persons number 1 and 2, and identification is hence not realiable. The features chosen for this experiment (mean, standard deviation, minimum and maximum) do not capture the characteristics of the signals adequately.
6. CONCLUSIONS
In this paper, the initial experiments on identifying persons based on their footsteps on an EMFi floor were reported. The results are very promising, but there are still many unanswered questions. In this phase, the basic tools for using the EMFi floor are being developed.
It is clear that the identification of three persons’ footsteps is not adequate to enable generalization of the results to a larger population. Therefore, another data set has already been collected, and it contains the measurements of 37 persons. Also,
another data set has been collected for studying the modelling of steps in the crossings of EMFi stripes. The data set includes footsteps with and without shoes, test material for studying steps using left/right foot, and the effect of the distance from the measurement device.
The features chosen for modelling (mean, standard deviation, minimum and maximum) were not able to capture the signal characteristics. Therefore, different features will be tested later on. Furthermore, the amount of data is too a small to allow HMM classification. Completely different classification methods will be tested and compared.
The problem of identification will be even more difficult with several persons walking in the room at the same time. This requires a methodology for tracking objects on the floor, and this will be studied in a different setting later on.
7. ACKNOWLEDGEMENTS
This work was funded by TEKES and Academy of Finland. The authors would like to thank Kalle Koho for his work on signal segmentation and EMFi data collection.
8. REFERENCES
- I. A. Essa, “Ubiquitous sensing for smart and aware environments: Technologies towards the building of an aware home,” IEEE Personal Communications, October 2000, Special issue on networking the physical world.
- “MIT’s oxygen project,” https://oxygen.lcs.mit.edu/, Available 22.1.2003.
- “Aware home,” https://www.cc.gatech.edu/fce/ahri/, Available 22.1.2003.
- M.D. Addlesee, A. Jones, F. Livesey, and F. Samaria, “ORL active floor,” IEEE Personal Communications, vol. 4, no. 5, pp. 35–41, October 1997.
- R.J. Orr and G.D. Abowd, “The smart floor: A mechanism for natural user identification and tracking,” in Proc. 2000 Conf. Human Factors in Computing Systems (CHI 2000), New York, 2000, ACM Press.
- M. Paajanen, J. Lekkala, and K. Kirjavainen, “Electromechanical film (EMFi) – a new multipurpose electret material,” Sensors and actuators A, vol. 84, no. 1-2, August 2000.
- S.E. Levinson, L.R. Rabiner, and M.M. Sondhi, “An introduction to the application of the theory of probabilistic functions of a Markov process to automatic speech recognition,” Bell Syst. Tech. J., vol. 62, no. 4, pp. 1035–1074, April 1983.
- V.-M. M¨antyl¨a, J. M¨antyj¨arvi, T. Sepp¨anen, and E. Tuulari, “Hand gesture recognition of a mobile device user,” in IEEE International Conference on Multimedia and Expo, 2000. ICME 2000., 30 July-2 Aug. 2000, vol. 1, pp. 281 – 284.
[9]
- H. Shatkay and L.P. Kaelbling, “Learning geometrically-constrained hidden markov models for robot navigation: Bridging the topologicalgeometrical gap,” J. Artificial Intelligence Research, vol. 16, pp. 167–207, 2002.
[10]
- L.R. Rabiner, “A tutorial on Hidden Markov Models and selected applications in speech recognition,” in Proc. IEEE, 1989, vol. 77, pp. 257–286.
[11]
- R. Bakis, “Continuous speech word recognition via centisecond acoustic states,” in Proc. ASA Meeting, 1976.
[12]
- F. Jelinek, “Continuous speech recognition by statistical methods,” in Proc. IEEE, 1976, pp. 532–536.
[13]
- V. Cherkassky and F. Mulier, Learning From Data. Concepts, Theory, and Methods., John Wiley & sons, Inc., 1998.
[14]
- L.E. Baum, “Statistical inference for probabilistic functions of finite state markov chains,” Ann. Math. Stat., vol. 37, pp. 1554–1563, 1966.
[15]
- A.P. Dempster and N.M. Laird amd D.B. Rubin, “Maximum likelihood from incomplete data via the EM algorithm,” J. Royal Statistical Society, vol. 39, no. 1, pp. 1–22, 1977.
[16]
- A.J. Viterbi, “Error bounds for convolutional codes and an asymptotically optimal decoding algorithm,” IEEE Trans. Informat. Theory, vol. IT-13, pp. 260– 269, 1967.
[17]
- S.J. Young, “The HTK Hidden Markov Model Toolkit: Design and philosophy,” Tech. Rep., University of Cambridge Eng. Dept., 1993, Tech. rep. TR.153.
[18]
- P. Heinonen and Y. Neuvo, “FIR-median hybrid filters,” IEEE Trans. Acoust., Speech, Signal Processing, vol. ASSAP-35, no. 6, pp. 832–838, 1987.


