Corydon D. Hilton
John J. Lesko, Chair
Scott W. Case
Mike W. Ellis
Saad A. Ragab
Surot Thangjitham
Abstract
Multifunctional material systems are systems that contain individual materials or components which are capable of performing multiple functions. The combination of functions into single entities allows for system-level benefits that are not possible through the optimization of subsystems independently. Benefits enabled through multifunctional designs include increased system efficiency through mass and or volume savings as well as part count reductions. Fiber reinforced polymer (FRP) composite materials are lightweight, high-strength materials that can be tailored to achieve a unique set of properties. These characteristics make composites ideal materials for multifunctional designs.
The current research focuses on the production, optimization, and characterization of a multifunctional fuel cell system. This product combines fuel cell technology with composite materials technology to achieve a design that produces electrical power while also providing specific load carrying capability. The study investigates new system designs and new processing techniques, including vacuum assisted resin transfer molding (VARTM) and pultrusion. A metric which allows for the characterization of multifunctional fuel cell systems is developed and applied to three fuel cell designs. This metric uses Frostig’s Higher Order Theory to analyze the mechanical behavior of the cells while the electrical performance of each device is based on its specific power output. For the cells investigated here, multifunctional efficiencies between 22% and 69% are achieved. The multifunctional efficiency is highly dependent on the transverse pressure applied to the fuel cell components, as this pressure determines ohmic resistances, mass transfer properties, and sealing abilities of the systems. The mechanical pressures at the GDL/Polar Plate interface of a model fuel cell system are explored via experiments with pressure-sensitive film as well as FEA studies, and an optimum structural pressure of approximately 200 psi is identified. Additionally, the effects that concentrated, bending loads have on the electrochemical performance of a model multifunctional cell are explored. The results indicate that one must give generous consideration to the out of plane loads which the fuel cell system will be subjected to (both inherent, structural loads resulting from processing conditions and external, applied loads encountered during operation) in order to achieve optimal multifunctional efficiency.
1. Introduction
Multifunctional designs allow for the combination of multiple system functions into a single material or system component. These designs allow benefits such as increased system efficiency through mass and/or volume savings, and reductions in system complexity/part count. The applications of this design concept are limitless. This is a major research area for the U.S. Army as military systems have an increasing demand for more efficient use of material mass and volume. For example, one goal that the army has is to replace the 80-ton M1A2 tank with a 20-ton vehicle. In order to meet this goal, it is imperative that material mass/volume be used very efficiently. One area in which the multifunctional design concept has gained considerable interest is with energy generation/storage. Next-generation ground vehicles will require large battery banks as they will utilize hybrid powertrains. The electronics (sensing and communication equipment) which soldiers use continue to become more complex and require additional power. The range and speed of unmanned aerial vehicles is currently limited by battery life. Many of these military systems also require a certain level of mechanical integrity, and therefore, the development of multifunctional systems which combine energy generation/production with some structural properties could prove beneficial over a wide range of platforms.
This dissertation will focus on multifunctionality and its potential in fuel cell technology. A multifunctional fuel cell, a fuel cell which, in addition to producing power, is also capable of withstanding structural loads, may offer significant benefits to many systems, including unmanned aerial vehicles, as mentioned above. Structural fuel cell research has been performed by the U.S. Army, and the current document aims to build upon these efforts in order to advance the technology. The Army has explored the use of the hand layup process to produce structural, composite fuel cells. These cells included carbon fiber/epoxy prepreg skins, aluminum foam current collectors/reactant distributors, and commercial membrane electrode assemblies. The current study recognizes areas in this technology where opportunity for advancement exists. For example, aluminum foam will corrode in a fuel cell environment, and therefore alternative materials exist which are more suitable for this application. Additionally, the hand layup process is very labor intensive, and alternative techniques may allow for more efficient manufacture of structural fuel cells. Beyond this, there is no fundamental research in this specific area which may be used to guide design efforts (so that optimum performance is achieved). Finally, there is a need for a metric which can be used to assess the multifunctional performance of these systems. Accordingly, key goals of this dissertation are to develop new materials and processing techniques for this technology, to investigate optimization of the electrochemical performance of the cells (as a function of applied assembly pressure), to achieve some understanding of the influence that mechanical loads have on electrochemical behavior, and finally, to develop a metric which can be used to characterize the performance of these multifunctional systems.
2. Literature Review
A brief review of the relevant literature will now be presented. First, the concept of multifunctionality will be discussed. This discussion will include benefits of multifunctional designs as well as organizations that are involved in the research. Next, a review of research efforts in multifunctional energy generation/storage will be presented. The review will include studies on multifunctional batteries, multifunctional capacitors, and multifunctional fuel cells. This will lead into a discussion of the areas that the current dissertation will address in order to advance the state of the field.
2.1 Multifunctionality
Multifunctionality is a concept that involves the development of new materials or devices which are capable of performing multiple functions within a system. The performance of the multifunctional device may be inferior to that of the monofunctional device, however, beneficial system level mass or volume saving
s may be achieved because the material elements perform multiple functions simultaneously. In other words, the combination of functions into a single material/device may permit overall improvements in system performance which may not be possible through optimization of subsystems independently [1, 2]. These functions may be related to the thermal, chemical, electrical, mechanical, and/or electromagnetic requirements of the system [3]. For example, U.S. Army subsystem functions may include structural support, ballistic protection, energy storage, power generation, power and data transmission, and communication [2]. In applications such as spacecraft, mass savings allowed through multifunctionality can drastically reduce launch costs [4]. It may be difficult to find homogeneous materials that satisfy multifunctional requirements. Because of the unique properties that they can be tailored to achieve, composite materials are ideal for multifunctional applications [3, 5]. Intense research on multifunctional energy generation and energy storage technologies has been conducted by scientists associated with organizations such as the U.S. Army Research Laboratory, the Air Force Research Laboratory, the Naval Research Laboratory, and Lockheed Martin Astronautics as they prepare for lighter, more efficient, next generation systems [2, 4, 6-10].
2.2 Multifunctional Energy Devices
Research related to multifunctional energy storage/generation will now be reviewed. This will include efforts to combine structural integrity with battery, fuel cell, and capacitor technologies.
2.2.1.1 Army Research Laboratory’s Battery
Researchers at the U.S. Army Research Laboratory have developed structural lithium-ion batteries. These multifunctional batteries were constructed by combining ion-conductive polymer electrolytes with continuous fiber reinforcement. The batteries contained an anode composed of carbon fabric, a cathode composed of a metal mesh coated with a lithium donor material, a glass fabric used as a separator layer, and a structural polymer electrolyte material doped with lithium salts. A schematic of the structural battery is shown in Figure 1.
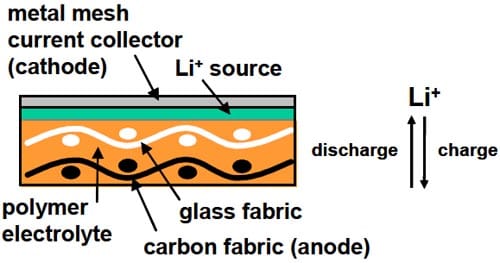
Figure 1. Schematic of multifunctional battery components
The researchers aimed to use materials that displayed a balance of electrical and mechanical integrity. The electrodes were required to sustain loads as well as to conduct electrons. The glass fabric separator was also required to sustain mechanical loads while serving as an electrical insulator between the battery’s electrodes. The structural electrolyte was required to achieve a balance of structural and ion-conductive properties. The components of the battery were consolidated using a modified vacuum-assisted resin transfer molding (VARTM) technique. A photograph of a nonfunctional prototype that was fabricated using this process is shown in Figure 2 [11].

Figure 2. Nonfunctional multifunctional battery prototype
The authors focused their electrolyte investigation on resins that included oligo(oxyethylene) units due to the well known ion conducting abilities of poly(ethylene glycol), PEG, in addition to the ease with which lithium salts may be dissolved into the PEG oligomers. The authors tested pellets of the electrolyte material systems for their ion conductivity and their compressive stiffness in order to identify the system that provided the optimal balance between the two properties. Data collected from impedance spectroscopy measurements over a frequency range of 10 Hz to 106 Hz at 20°C was used to obtain conductivity values for the potential electrolyte materials while uniaxial compression testing was used to investigate the stiffness of the materials.
The investigation of the polymer electrolyte systems was continued by the scientists in a report by Snyder et al. [6]. In this report, prismatic bars of potential electrolyte systems were formed and tested through dynamic mechanical analysis (DMA). DMA testing was conducted at temperatures ranging from -135°C to 150°C at a frequency of 1 Hz. Figures 3 and 4 show conductivity versus compressive modulus and storage modulus, respectively, for the polymer electrolytes investigated in the study.
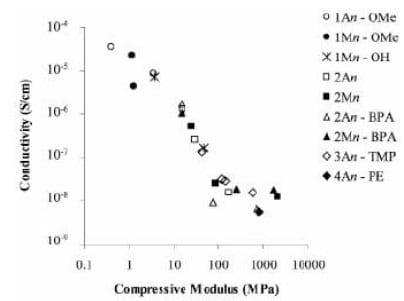
Figure 3. Conductivity vs. Compressive Modulus for various electrolyte systems
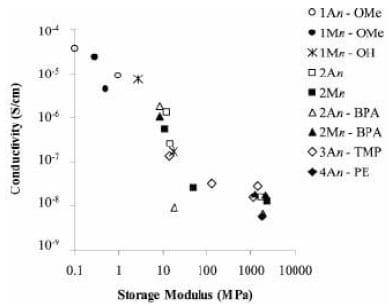
Figure 4. Conductivity vs. Storage Modulus for various electrolyte systems
Figures 3 and 4 display the multifunctional character of the polymer electrolyte systems. Systems that lie along the y-axes (represented as having a compressive modulus or storage modulus of 0) may be considered commercial liquid electrolytes while those that lie along the x-axes (represented as having a conductivity of 0) may be considered to be structural resins. Samples with higher multifunctionality will tend to display a combination of both properties and will therefore tend toward the upper-right portion of the plots. In general, the electrochemical-mechanical properties for most of the samples were about an order of magnitude below what would be required for multifunctional applications. The researchers concluded that generally speaking, those systems that were highly conductive were structurally weak while and those that were poorly conductive tended to be highly structural materials. The results suggested that a neat homopolymer electrolyte will unlikely satisfy structural requirements, and that, combining monomers or different properties as copolymers will be more likely to achieve multifunctional standards.
2.2.1.2 Boundless Corporation’s Battery
Boundless Corp., Boulder, Colo., has also developed a multifunctional lithium-ion battery. The Missile Defense Agency funded this research for potential application in their onboard power systems. The company also sees potential for the technology in spacecraft, unmanned aerial vehicles, and automobiles. The battery is based on partially saturated carbon composites. One face of the single-layer composite is fully saturated for stiffness and strength while the other face is uncoated carbon fiber. The entire surface area of this face is used for ion intercalation, or insertion. Fibers run continuously into and out of the resin. This allows for conductivity throughout the battery, even through the saturated portion of the composite. The battery is shown in Figure 5. Boundless researchers have a goal of delivering battery power performance up to 5 kW/kg [12].

Figure 5. Boundless Corp.’s multifunctional lithium-ion battery
2.2.1.3 Naval Research Laboratory’s Battery
Researchers at the Naval Research Laboratory and Geo-Centers, Inc. [1, 13, 14] have also investigated the benefits made possible through the development of a structure battery multifunctional design . The intended use of the design is for unmanned air vehicles (UAVs) in general. Particular focus has been put on incorporating the design into the Black-Widow Micro-Air-Vehicle (MAV). The Black-Widow MAV weighs 81 grams, 50 of which are structure and battery. The fuselage is a monocoque shell design of expanded polystyrene foam. The goal of the effort is to replace the current batteries, fiberglass carriage structure, and parts of the p
olystyrene fuselage with a structure-battery design in order to increase flight endurance time. Currently, the Black-Widow’s flight endurance time is 30 minutes for steady-level cruise conditions at approximately 30 mph. The flight endurance time, tMAV is given by
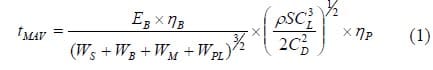
where EB is the energy capacity of the battery and ηB is the efficiency factor that accounts for the current draw rate, temperature, etc.; WS,B,M,PL are the weight of the structure, battery, motor, and payload, respectively; ρ is the density of air; S is the wing platform area; CL and CD are the lift and drag coefficients, respectively; and ηP is the propeller efficiency. Equation 1 shows that the flight endurance time is directly related to the energy capacity and efficiency factor of the battery, as well as the weights of the structure and the battery. The normalized change in endurance time with changes in energy and changes in the weights of the structure and battery is
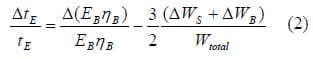
This equation shows that decreasing the weight is 1.5 times more effective in increasing the endurance time than increasing the battery energy.
The proposed design will use a thin-layer, polymer lithium-ion (PLI), rechargeable battery system developed by Telcordia Technologies. The batteries are available in a unicell or bicell configuration. The bicell configuration was chosen for this effort as this configuration has a higher specific energy and energy density. Figure 6 shows a plot of energy storage abilities of various battery systems.
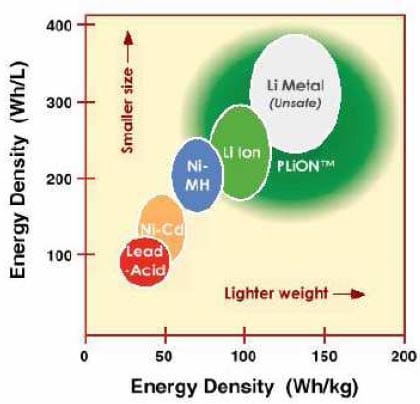
Figure 6. Energy storage abilities of various battery technologies. PLiONTM refers to the Telcordia plastic-lithium-ion bicell.
The bicell configuration consists of three active layers which are laminated together and have a nominal total thickness of approximately 0.054 cm. A schematic of the bicell is shown in Figure 7.
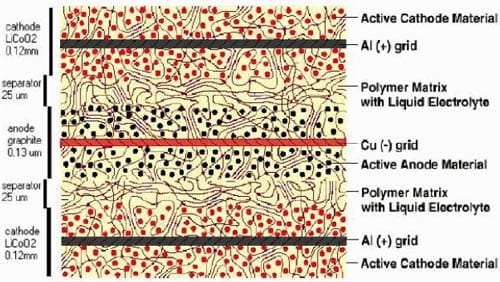
Figure 7. Telcordia Technologies’ PLI bicell configuration
One or more outer layers of special packaging and structural additives are incorporated to provide mechanical integrity to the system. An in-house Multidisciplinary Design Optimization (MDO) code was used to determine the subsystem specifications and parameter settings in order to achieve maximum flight time. The results of tests on various designs showed that one of the optimized PLI designs predicted a flight endurance time of 70 minutes, over twice the flight time of the current design.
Qidwai et. al. [15] investigated actual end-user solutions for the application of multifunctional thin film lithium-ion polymer battery cells. The investigation centered on testing possible end-user concepts for UAVs. Four commercially available solid polymer lithium-ion batteries were evaluated for mechanical and electrical properties. The four batteries tested were made by Kokam, Philips, Thunder Power, and E-Tec. They were of comparable geometry, size, and charge capacity as shown in Figure 8.
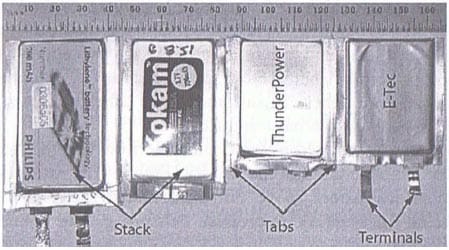
Figure 8. Four commercial batteries tested for mechanical and electrical performance
As integration of these batteries into a larger structure requires some sort of bond between the battery packaging and its mating substrate material, testing of various bonding agents was also performed. Shear stiffness and flexural stiffness of the cells were also investigated in custom setups which mimicked potential application setups. Specific power vs. specific energy plots were generated for the four battery types as well. The authors concluded that these commercial batteries are capable of withstanding large deformations without degradation of energy-storage performance. Results of the mechanical and electrical testing showed that the Thunder Power cells outperformed the other cells, followed by Kokam and E-Tec.
2.2.1.4 Air Force Research Laboratory’s Battery
Cost restrictions on advanced military and commercial space systems demand increased efficiency in spacecraft subsystems in order to reach higher payload mass fractions. The Air Force Research Laboratory has developed a Multifunctional Structures (MFS) concept to create weight and volume savings that will enable next generation systems. Under a contract between the Air Force Research Laboratory and ITN Energy Systems, Inc., a next generation spacecraft battery technology is under development. Lithium Battery Core, or LiBaCore, is the name given to a thin-film, solid battery that is deposited on an aluminum foil substrate in the form of a continuous ribbon. This system has the potential to be used in applications such as solid state memories and in medical devices such as pacemakers. Through the integration of the LiBaCore battery into the honeycomb panel, next generation spacecraft such as the TechSat 21, can minimize mass, packaging volume, and cost. The solid state lithium battery chemistry results in a cell specific energy of 200 W-hr/kg. This may be compared to 50 W-hr/kg for conventional liquid chemistries. Additionally, the need for battery sleeves, mounting inserts, and the requirement of isothermalization are eliminated. This reduction in required parts creates additional mass savings. [4].
2.2.1.5 The Future of the Multifunctional Battery
The future of the multifunctional structural battery will face many challenges. The biggest bottleneck in the development of multifunctional structural batteries is the procurement of the custom cells. Presently, there are only a few manufacturers of polymer lithium-ion systems that are willing to consider manufacturing custom cells. These small custom runs usually produce many fewer cells than commercial battery runs, and it can become expensive to produce the custom cells. A custom cell that may be used in a multifunctional structural application can cost several thousand dollars. Reducing this cost is one of the goals of the multifunctional battery efforts. Optimizing the multifunctional performance of the structures is another challenge. From a structural viewpoint, achievement of good load transfer from the structure to the structure-battery packaging to the energy-storage materials inside of the packaging, without negatively impacting both short term performance and long term durability, is a major issue. Electrically, the technology must attain higher specific energies with corresponding increases in specific power, which is already a major research effort within the energy storage research community [16].
2.2.2 Multifunctional Fuel Cell
The battery is similar to the fuel cell in that both generate electrical energy from chemical energy. The main difference is that the battery cell contains chemical reactants while the reactants are supplied to the fuel cell from outside of the cell. Research activity related to direct methanol fuel cells (DMFCs) has grown exponentially over the last 15 years. The DMFC is considered to be the most promising fuel cell to become a replacement for the battery. It has potential to offer 10 times higher power densities than current lithium-ion rechargeable batteries [17, 18].
2.2.2.1 Army Research Laboratory’s Fuel Cell
Researchers at the U.S. Army Research Laboratory have also developed multifunctional DMFCs which were
designed to provide mechanical integrity while producing power. The cells were constructed in a composite sandwich structure form [11]. These structures have been proven to be excellent candidates for the attainment of multifunctional designs [19, 20]. The DMFCs consisted of polymer matrix composite skins and a structural fuel cell core. A schematic of the structural fuel cell is shown along with a picture of the actual cell in Figure 9.
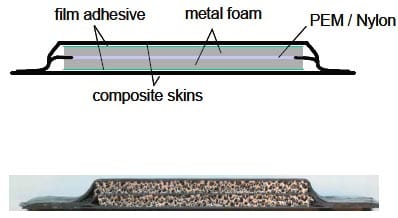
Figure 9. Schematic of multifunctional fuel cell along with actual photograph of cell.
A carbon fiber-epoxy prepreg was used for the composite skins while open cell aluminum foam and a standard membrane electrode assembly (MEA) were placed into the core location. The foam core served as a distribution medium in order for the fuel and air reactants to reach the MEA. It also served as an electron conductor while providing shear and compressive stiffness for the structure. The density and porosity of the aluminum foam were varied to identify an optimal balance of mechanical and electrical integrity. The components of the fuel cell were consolidated using a hand layup process. The composite was then cured under vacuum at 120°C for one hour. 3 point bending experiments were performed with various aluminum foams to investigate the bending stiffness properties of the multifunctional fuel cell structure. Various foam- MEA arrangements placed into a polycarbonate fixture were used along with a test station by Fuel Cell Technologies to generate voltage-current (V-I) curves. A 2 M methanol solution (8% by volume) was pumped at a flow rate of 2 cm3/min while air at 20°C was supplied at 400 standard cubic centimeters per minute. Results of the electrochemical experiments are shown in the figure below.
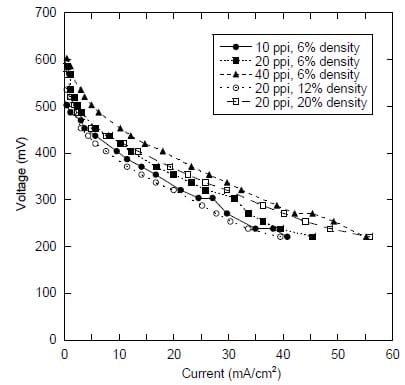
Figure 10. V-I curves obtained from various foam porosities and densities
Results of the mechanical and electrochemical testing showed that the best overall multifunctional performance was achieved with the foams of higher porosity or higher density [21].
2.2.2.2 Multifunctional Electrodes for Fuel Cells
Kaempgen et. al. [22] developed multifunctional carbon nanotubes to be used as electrodes in fuel cells. Dense single wall carbon nanotube (SWCNT) networks are highly conductive, have high surface area, and high porosity. These properties make these networks attractive materials for electrodes in various electrochemical devices. Amorphous carbon (a-C), which is currently a state of the art material for electrodes, requires binders and mechanical support at the backside, such as a woven carbon cloth or metallic mesh. The SWCNT form a freestanding film without any additive or support. The network structure formed by the nanotubes is also more robust in terms of bending and abrasion. In this research, the authors completely replaced the a-C material by SWCNT networks and demonstrated that the networks provide the necessary functions for fuel cell operation including gas diffusion, catalyst support, electrolyte contact, and current collection. The use of the SWCNTs simplifies manufacturing and requires less material which leads to extremely thin and lightweight gas diffusion electrodes. Comparisons between the SWCNT network electrodes and a-C electrodes showed that conductivity increased by more than two orders of magnitudes while thickness and mass decreased by more than one order of magnitude when the SWCNT network electrodes were used.
2.2.2.3 The Future of the Multifunctional Fuel Cell
The research performed has shown that the construction of multifunctional fuel cells is possible and that significant challenges remain in the development of the structures. The scientists at the Army Research Laboratory site core geometry as a major issue that needs to be addressed in order to improve the performance of the fuel cell. The cores should be engineered to minimize the effect that the midplane membrane has on shear strength. Shear connectors at the midplane could help to optimize the mechanical performance of the cell. Interdisciplinary coordination and cooperation will be required for the general conception, design, and implementation of the multifunctional fuel cell. Other major obstacles that must be overcome in the advancement of the multifunctional fuel cell include the development of new materials, material architectures, and fabrication techniques [11, 21].
2.2.3 Multifunctional Capacitor
Research on the development and analysis of multifunctional capacitors is reported by O’Brien et al. [8] and Baechle et al. [23]. These capacitors were designed to achieve structural integrity while displaying capacitive energy density. To form the capacitors, electrically conductive electrode layers were placed between composite dielectric plies. The edge of the electrode was extended past the edge of the composite dielectric material to allow for electrical connections and bussing. The researchers tested a variety of composite dielectric materials. A schematic of the multifunctional capacitor is shown in the figure below.
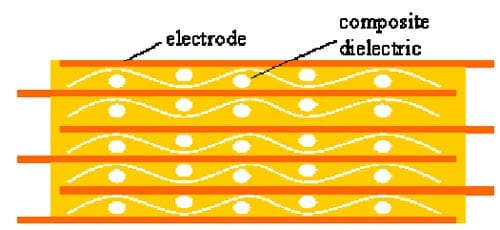
Figure 11. Schematic of multifunctional capacitor
O’Brien et al. [8] manufactured three types of specimens from prepreg. Two were manufactured using conventional structural composite prepregs. These included a woven glass-polyester (Cycom 4102, Cytec Ind, West Patterson, NJ) and a unidirectional glassepoxy (BT250E, Bryte Technologies, Morgan Hill, CA). A third was manufactured from a prepreg that is typically used to make circuit boards (N4205-6FC, Nelcote, Inc, Waterbury, CT)– referred to by the authors as glass-FR4. The material is made from a brominated, fire-resistant epoxy and is much thinner than typical structural prepreg. Aluminum-coated polyimide was used as the electrode material. Samples of varying dielectric thickness (varying number of plies) were manufactured so that the effect of dielectric thickness on capacitor performance could be investigated. The components of the capacitor were consolidated with a hot press by ramping at 3°C/min to 121°C (250°F) for 2 hours at 345 kPa (50 psi). Hot press cycles were also used to consolidate the capacitors manufactured using E-glass with various matrix materials. The electrodes were subsequently covered with copper tape in order to improve their durability. A schematic of the structural capacitor including component dimensions is shown along with a photo of an actual capacitor in Figure 12.

Figure 12. Schematic of multifunctional capacitor (including dimensions) and photograph of multifunctional capacitor manufactured from FR4 prepreg
An LCR meter was used to measure the capacitance of all specimens at 1 kHz. The dielectric breakdown strength, which is an important quantity in the calculation of the capacitor’s energy density, of the capacitor samples was determined by ramping the voltage across the specimens up until failure. Tensile tests on a load frame with a 5 kN load cell were used to determine the stiffness of the multifunctional specimens. The researchers also developed a multifunctional metric based on the structural properties and the capacitive properties of the structural capacitors. Using this metric, the authors were able to determine the overall multifunctional efficiency of each capacitor design.


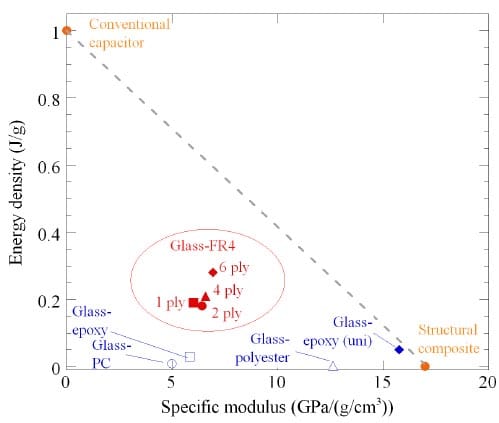
Figure 13. Energy density vs. specific modulus for various structural capacitors.
The energy density axis represents how well the multifunctional capacitor performs as a capacitor while the specific modulus represents how well the device performs as a structure. An energy density of 1 J/g is representative of a conventional capacitor while a specific modulus of 17 Gpa/(g/cm3) is taken to be representative of a structural composite. The dashed line represents a critical multifunctional efficiency for the structural capacitor. Above this line, overall weight savings are achieved in the system, while below this line, weight savings are not achieved, as described by Equation 4. As the plot shows, none the systems tested in this study achieved system level weight savings.
In summary, the potential benefits of multifunctional energy generation/storage have been recognized by many organizations and have drawn a great deal of research interest. The development of new materials, material architectures, and processing methods have been identified as areas that will aid in the advancement of the multifunctional fuel cell. In addition, design/parameter optimization studies and the development of a characterization method (such as that which has been discussed for the structural capacitor) are key to the progression of the multifunctional fuel cell.
3. Objective of the Research
The objective of the current research is to make a significant contribution to the advancement of multifunctional energy generation technology. In this effort, particular focus is placed on the multifunctional fuel cell. The goals of the study follow.
- The development of new processing techniques (VARTM and pultrusion) and cell designs. Additionally, the development of a metric which may be used to measure the multifunctional efficiency of the structures is essential.
- An understanding of the influence that inherent, structural pressure has on the electrochemical performance of the system as this may be used to aid in the design of these multifunctional systems.
- An understanding of the effects that transverse loads may have on the electrochemical performance of the cell. In particular, the mechanical loads of interest here are the inherent, structural load and an external, applied bending load.
The three chapters that immediately follow discuss efforts to achieve the stated goals. Chapter 4 describes efforts made to accomplish the first objective. It describes various multifunctional fuel cell designs and presents a metric by which the designs are characterized. The second goal is discussed in Chapter 5, which deals with efforts to achieve improved cell performance by investigating the influence that assembly pressure has electrochemical performance of a structural fuel cell design. The final objective is considered in Chapter 6, which explores the effects that structural pressure loads and 3 point bending loads have on the electrochemical characteristics of a multifunctional fuel cell system.
4. Characterization of Multifunctional Fuel Cell Designs
4.1 Abstract
The U.S. Army has investigated various multifunctional designs in order to achieve system level mass and/or volume savings. One of the multifunctional devices developed is the multifunctional fuel cell – a fuel cell which simultaneously provides a system with structural support and power generation. However, there are no established methods for measuring how well a particular design performs or its multifunctional advantage. The current paper describes multifunctional fuel cell designs which have been manufactured based on a goal of providing mass savings for a system and presents a metric by which designs such as these can be characterized. The mechanical aspect of the metric is based on the specific bending stiffness of the structural cell and is developed using Frostig’s Higher Order Theory. The electrical component of the metric is based on the specific power density achieved by the structural cell. The structural systems considered here display multifunctional efficiencies ranging from 22% to 69%. The higher efficiency was obtained by optimizing the contact pressure at the GDL in a model cell design.
4.2 Introduction
The multifunctional design concept offers a new way of thinking regarding the development of U.S. Army systems. In these designs, single components/materials perform multiple functions for the system. These functions may be of a mechanical, electrical, chemical, thermal, and/or electromagnetic nature [3]. For example, the subsystem functions of importance to the U.S. Army include structural support, ballistic protection, energy storage, power generation, power and data transmission, and communication [2]. Intense research on multifunctional energy generation and energy storage has been conducted by scientists working with many organizations, including the U.S. Army Research Laboratory, the Air Force Research Laboratory, the Naval Research Laboratory, and Lockheed Martin Astronautics [2, 4, 6-10]. The current study focuses on multifunctional fuel cell designs which may allow for system level mass savings. These devices not only generate power, but also (simultaneously) provide a system with structural support.
Composite materials are ideal for multifunctional designs because of the unique properties which they can be tailored to achieve [3, 5]. The multifunctional fuel cells considered here are of a sandwich structure design as they consist of composite facesheets along with lightweight, foam core materials. An illustration of this design idea is provided in Figure 14. The external composite structure is designed to isolate the fuel cell from shear and bending loads which may affect the performance of the fuel cell. Sandwich structures are used in many structural applications because of the high specific bending stiffness and strength that is characteristic of the designs [24-26].
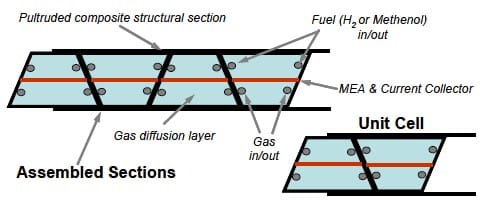
Figure 14. Pultrusion structural fuel cell system concept
In the current study, we consider our multifunctional fuel cell designs as they are subjected to 3 point bending loads. Frostig et al. [27] have developed a High-Order Theory which is capable of accurately analyzing the behavior of these sandwich structures. This theory accounts for the nonlinear deformation of modern, soft core materials and therefore represents sandwich beam behavior more accurately than classical approaches. A great deal of literature is available in which this high order analysis has been used to investigate bending of sandwich beams structures [26-34].
The current study examines structural fuel cells – devices which display both mechanical integrity and the ability to produce power. The potential of sandwich structure design technology to produce these multifunctional cells is shown. A variety of structural sandwich materials and fuel cell materials are investigated. Two glass fiber composite facesheets are used along with Diab Divinycell and Trymer foam materials. Aluminum foam, carbon foam, and custom graphite fiber composite materials are used as polar plates. The potential of VARTM (Vacuum Assisted Resin Transfer Molding) and pultrusion as processing techniques for these devices is demonstrated. We initiate the discussion by proposing a multifunctional metric which is used as a characterization tool for the structural fuel cells.
4.3 Multifunctional Metric for Fuel Cell
In order to access the performance of multifunctional technologies, it is necessary to have a metric which considers all of the desired functions for the device. Following the method used by O’Brien et al. [8] for a structural capacitor, we propose a multifunctional metric for the structural fuel cell. O’Brien et al. consider a capacitor-structure of constant cross section which is loaded in tension. The expression for the mechanical stiffness of the structure is based on classical hookean elasticity and uses the specific modulus, E (in Pa·m3/kg), of the system as the structural design parameter. Energy density (in J/kg), is used to characterize the capacitive performance of the system. An improved multifunctional design is considered as a design that maintains overall system stiffness and energy storage while reducing the weight of the system.
The metric proposed here is applicable to multifunctional fuel cells which are designed as sandwich structures. The systems considered are of constant cross section and are subjected to bending (3-point bending) loads. In order to characterize the stiffness of the structures, Frostig’s High-Order Sandwich Theory is employed. This theory improves on classical and superposition theories as it recognizes the nonlinear distribution of vertical and longitudinal deformations through the height of the core. This nonlinear behavior must be considered when transversely flexible cores are considered [27].
We will begin our metric development by defining a system design where the total mass is the mass of fuel cells mfc and the mass of the structure, ms:
The specific stiffness of the faces, the specific compressive stiffness of the core, and the specific shear stiffness of the core will be used as structural design parameters for the multifunctional fuel cell. They are defined as

Note that for the sandwich structures analyzed in the current study, we will assume that the skins provide the structure’s bending stiffness and that the core provides the system with shear stiffness and transverse stiffness – as discussed by Frostig [27]. We now consider a sandwich structure of constant cross section and of length 2 L which is a simply supported beam with a pressure distribution load,

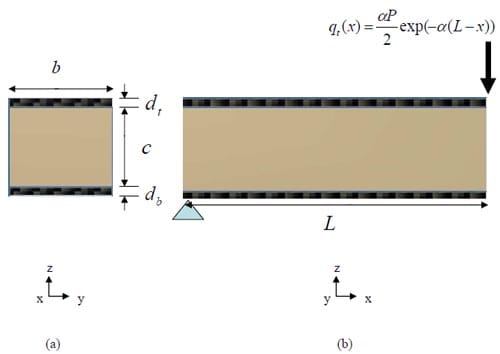
Figure 15. Geometry and Loading Details of Sandwich Structure: (a) Cross-sectional view of sandwich structure showing dimensions, (b) View along length of structure, including support and loading conditions (Note: Half symmetry is used in this illustration)
It can be shown that the deflection of the structure’s neutral axis is very close to the deflection of its bottom face and that the bottom face can therefore be used to accurately predict the stiffness (load/deflection) of the structure [25]. The overall system stiffness S (in N/mm) can be expressed follows (see Appendix A):


where the Ci , Cbi, and si values are obtained from the theory’s governing equations which can be expressed as

Note: For the calculation of i b values in the numerical code, face thicknesses are expressed as follows: dt = df is the thickness of the top face sheet, and db = df – (1e – 08) b f is the thickness of the bottom face sheet, in order to avoid solution failure due to a singularity in the coefficient matrix, as discussed by Swanson in [34].
Additionally, it should be noted that the stiffness of the structure, S, is actually independent of the concentrated load, P. This will become evident if the constants C1-C4 and Cb5-Cb12 are expressed explicitly – as they are a function of this applied load.
Removing the mass term,m , from the numerator of the system stiffness expression, we are left with a structural stiffness parameter which we will define as M (in MPa·mm/g).
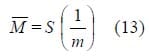
The design metric for the fuel cell’s electrochemical performance is the power density P (in W/g) with overall system power output defined as
In the new design, a multifunctional, structural fuel cell of mass sfc m supplements the monofunctional fuel cell and structure. The power density and stiffness parameter of the structural fuel cell are equal to s PP ands sM , respectively. s P and s s represent the power efficiency and structural efficiency of the structural fuel cell, respectively. It is required that σP < 1 and σS < 1, which indicates that the power efficiency and the structural efficiency of the multifunctional fuel cell will always be inferior to the respective values in the comparative monofunctional materials. For the multifunctional system, we assume that the mass of the monofunctional fuel cell and structure are reduced to m*fc < mfc and m*s < ms, so that total system performance can be summarized as follows.
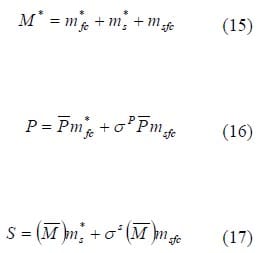
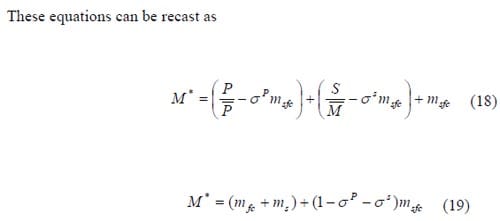
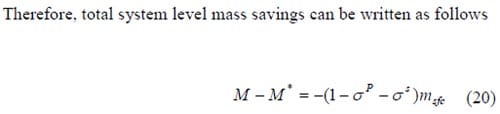
A structural fuel cell will therefore enable system level mass savings if
Let us consider a Direct Methanol Fuel Cell with length and width dimensions equal to 10 cm and 3 cm, respectively. A Nafion112 MEA with a 10 cm x 3 cm membrane area and a 9 cm x 2.5 cm active area is placed at the device’s midplane. The cell contains a 0.08-cm thick central portion which consists of the MEA along with 2 silicon gaskets. Using typical DMFC dimensions/properties including a total cell thickness of 0.3 cm, an area based power density of 14.3 mW/cm2 at room temperature [35], and a monopolar plate density of 1.88 g/cm3 along with an assumption that the monopolar plates account for 80% of the weight of the cell [36], we can obtain P = 26.7 mW/g as the mass-based power density for an average cell. The power effici
ency of the multifunctional fuel cell is given by
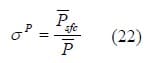
where Psfc is the structural cell’s mass-based power density. We will now consider a symmetric sandwich beam of high structural integrity which consists of woven glass (Rovcloth1854)/Derakane 510A-40 resin skins (Vf = 0.6) and a Divinycell H250 structural foam core. Dimensions include a beam length 304.8 mm, a beam width of 56 mm, a core thickness of 32 mm, and a skin thickness of 2.54 mm. This sandwich structure has a structural stiffness parameter value of M = 2.49 MPa x mm/g. The structural efficiency of the multifunctional fuel cell is given by:
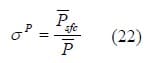
where Msfc is the structural fuel cell’s structural stiffness parameter.
4.3.1 Validation of Frostig’s Theory
The mid-plane distributions of shear and transverse normal stresses (along the length) of the VARTM cell are displayed in Figure 16. A cell with a length of 304.8 mm, a beam width of 56mm, a core thickness of 32 mm, and facesheet thickness of 2.54 mm was considered. The stresses correspond to a 3 point bending scenario where a concentrated load of 6000 N is applied at the structure’s center (x = 152.4). Results are presented from FEA studies and from the numerical code based on Frostig’s theory. In general, good agreement is observed between the two analysis techniques, and the FEA results validate the potency of Frostig’s Theory in analysis of bending in sandwich structures.

Figure 16. Mid-plane (a) shear and (b) transverse normal stress distributions in VARTM cell for a 3 point loading case with a concentrated central load of 6000 N
4.4. Experimental
4.4.1 Fuel Cell Designs
Multifunctional fuel cells have been manufactured through the VARTM and pultrusion composite processing methods. Additionally, a third design has been developed which uses a strong, lightweight carbon foam (KFOAM) material as a reactant distributor/electrical conductor. Extensive details on the processing/testing of the cells manufactured from VARTM and pultrusion has been given by Peairs et al. [37]. This information will be briefly reviewed here, and a discussion of the KFOAM-based design will be presented as well.
4.4.1.1 VARTM Cell
The first version of the multifunctional fuel cell was manufactured using the VARTM process. This cell included a commercial, custom Membrane Electrode Assembly (MEA). The MEA included a Nafion 112® membrane with carbon cloth GDLs on either side. The catalysts loadings for this MEA were 2.0 mg/cm2 Pt-Ru at the anode and 4.0 mg/cm2 Pt at the cathode side of the cell. An open cell aluminum foam material was used in this setup in order to distribute reactants and to conduct electrical charge. A piece of this foam was placed on each side of the MEA in the fuel cell setup. Rectangular brass tubes were used in order to carry reactants to and from MEA reaction sites. This tubing also served as a current collector in the fuel cell. Silicon gaskets were added in order to prevent reactant leaks, and a closed cell foam material (Divinycell H60) was placed on either side of the cell. These components were then wrapped with a plain weave glass fabric, and Derakane 510A-40 vinyl ester resin was added through the VARTM process in order to create the final structure. Figure 17 shows a cross sectional image of this multifunctional fuel cell.

Figure 17. Cross section of multifunctional fuel cell manufactured using VARTM method
4.4.1.2 Pultruded Cell
The pultrusion process was used to create the next version of the structural fuel cell. The components of this cell are shown in Figure 18. A custom MEA with a Nafion 117® membrane was obtained from fuelcellstore.com for the cell. The MEA consisted of carbon cloth GDLs and catalysts loading consistent with those used in the VARTM cell (2 mg/cm2 Pt-Ru at the anode and 4 mg/cm2 Pt at the cathode). Channeled 60% graphite/40% polyphenylene sulfide monopolar plates were manufactured through compression molding (at 300°C) with a custom aluminum mold. Two holes were drilled through each plate after the molding process to allow for custom PVC fittings which were used as reactant inlets and outlets. Silicon gaskets were used to seal the cell. The assembly of the cell started with the MEA at the cell’s center. The MEA was first placed between two gaskets. Monopolar plates with attached fittings were then placed on either side of the MEA. This assembly was then placed into a polyisocyanurate foam insulation to prepare the assembly for processing. From the inside to the outside, the pultrusion materials consisted of the foam core/fuel cell assembly, an inner mat of E-Glass, glass rovings, and finally an outside mat. Holes were drilled through the composite skin of the final structure at the fitting locations to create inlets/outlets for the fuel and air reactants.
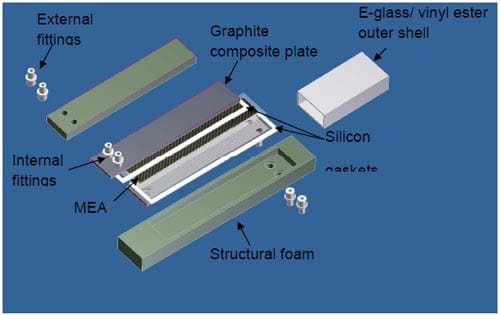
Figure 18. Illustration of pultruded fuel cell components
4.4.1.3 KFOAM Cell Design
Figure 19 shows the components of the carbon foam-based fuel cell design. A MEA with a Nafion 112® membrane was placed at the center of the assembly. The catalysts loading of this MEA was consistent with that of the VARTM and pultrusion designs. On either side of the MEA, gaskets were used to seal the cell. Gasket testing proved that a combination of two different gasket materials provided the best leak prevention in the cell. A Neoprene/EPDM/SBR gasket (“Gasket 1”) was used on the anode side of the cell and a silicon gasket (“Gasket 2”) was used on the cathode side of the cell. KFOAM materials were then placed on either side of the cell, and stainless steel sheets were used as current collectors. The fuel components were assembled in a fixture with polycarbonate plates in order to test the electrochemical performance of the cell. The length, width, and thickness dimensions of the polycarbonate plates were 12.7 cm, 8.5 cm, and 1.3 cm, respectively. Ten bolts were placed through holes in the plates to hold the assembly together. Two additional holes were placed in each plate and used as reactant inlets/outlets. The thickness of the stainless steel current collector sheets were 0.03 cm. The carbon foam pieces were machined to dimensions of 0.32 cm in thickness, 9 cm in length, and 2.5 cm in width.
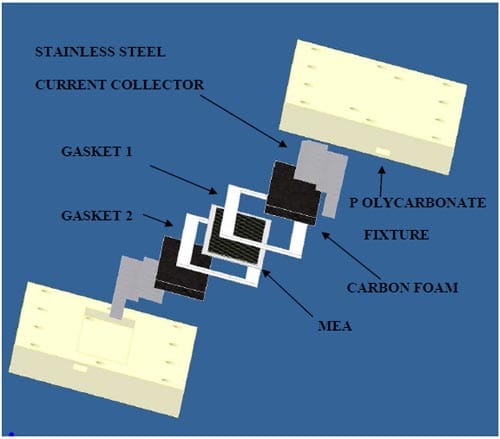
Figure 19. Components of carbon foam fuel cell design
4.4.2 Testing/Analysis of Fuel Cell Designs
The cell designs were tested for electrochemical performance with the aid of a fuel cell test station manufactured by Fuel Cell Technologies, Inc. All tests were conducted at room temperature. A 2 M methanol solution (8% methanol by volume/92% water) was used as the fuel for all tests. This fuel was supplied to the anode side of the cell at a flow rate of 2 mL/min using an external peristaltic pump. Humidified air was supplied to the cathode side of the cells at a flow rate of 500 SCCM. The KFOAM based design was tested in an external fixture which consisted of the components shown in Figure 19 along with additional aluminum endplates. The a
dditional endplates were placed outside of the polycarbonate plates in order to stiffen the fixture.
A numerical code based on Frostig’s High-Order Theory was used in addition to models developed in ANSYS to investigate the mechanical behavior of the fuel cell designs. The numerical code was based on Frostig’s 8th order solution to a 3 point loading case. Symmetry was used so that it was only necessary to analyze half of the beam, and a pressure distribution function (Equation 9) was used to apply the point load, as discussed by Swanson [34]. The theory was used to calculate the structural stiffness parameter for each of the fuel cell designs according to Equation 13. For the FEA studies, the sandwich structure components were modeled in two dimensions (no thickness), and PLANE 82 elements were used in the analyses. The mesh settings were considered acceptable as mesh refinements resulted in negligible changes in the calculated stresses. The concentrated load was approximated by a linear function which was applied to a very small section (0.2 mm) of the upper face sheet.
4.3 Results and Discussion
4.3.1 Electrochemical Performance/Power Efficiency
Figure 20 shows the electrochemical performance of the fuel cell designs investigated. The KFOAM fuel cell design shows great improvement relative to the designs manufactured through the VARTM and pultrusion processes. This is a result of extra care that was taken to optimize the interfacial contact pressures in this design – in an effort to improve the performance of the multifunctional cells, various studies were conducted in order to find an optimum contact pressure between the GDL and KFOAM material [38]. The power densities achieved by each cell are 0.54 mW/cm2 for the VARTM design, 0.6 mW/cm2 for the pultruded design, and 9.1 mW/cm2 for the KFOAM design. These densities correspond to mass-based power densities of 0.42 mW/g, 0.45 mW/g, and 4.58 mW/g for the VARTM, pultruded, and KFOAM designs, respectively. Using Equation 22, the power efficiencies for the designs are obtained as VARTM cell: 0.016, pultruded cell: 0.017, and KFOAM design: 0.17. (Note: As the KFOAM design has not yet been manufactured into a true composite structural fuel cell, values calculated here assumed foam and facesheet properties similar those used with VARTM cell.)
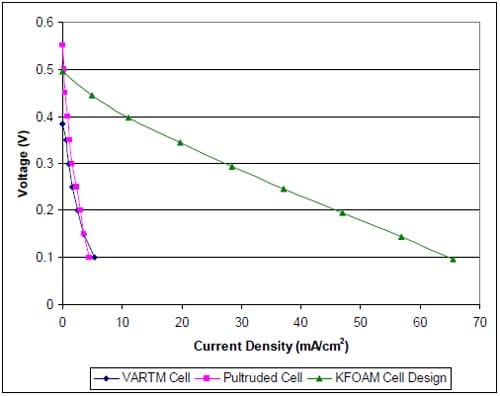
Figure 20. Polarization curves for the fuel cell designs
4.3.2 Mechanical Performance/Structural Efficiency
Table 1 contains the stiffness, S , (calculated according to Equation 10) values as well as values for the structural stiffness parameter, Msfc, (Equation 13) and the structural efficiencies, σs, for each of the multifunctional fuel cell designs. (As done in the power efficiency calculations, the multifunctional KFOAM design was considered to have cell components similar to those of the VARTM design).
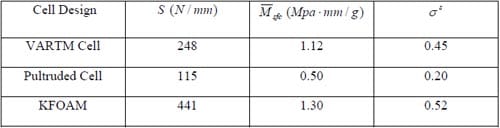
Table 1. Structural characterization parameters for multifunctional fuel cell designs
4.3.3 Multifunctional Efficiency
The multifunctional efficiencies of the structural fuel cell systems which were analyzed in this study are displayed in Figure 21. The multifunctional efficiencies achieved by the designs investigated here are 0.47, 0.22, and 0.69 for the VARTM, Pultruded, and KFOAM designs, respectively. The dashed line represents σmf = 1. As previously discussed, this is the critical point for system level mass savings. Systems which possess a multifunctional efficiency in the region below this line will not enable mass savings at the system level while those above this critical line will enable mass savings. All of the systems examined in the current study fall short of this critical s mf value. In particular, the systems investigated here display low power outputs/power efficiencies. This is likely due to high contact resistances at the GDL/polar plate interfaces in the VARTM and pultrusion cells as the structural pressures in these cells were not examined/optimized prior to the processing of the systems. This pressure has been optimized in the KFOAM cell, however, this cell contains multiple interface locations (between the GDL and the KFOAM as well as between the KFOAM and the stainless steel) where electrical losses may occur. These interfaces may limit the power output by the design, and slight modifications to the design may allow for increased multifunctional efficiency. Potential to improve the structural efficiency of all of the systems exists in the modification of system designs by incorporating lighter, stiffer materials.
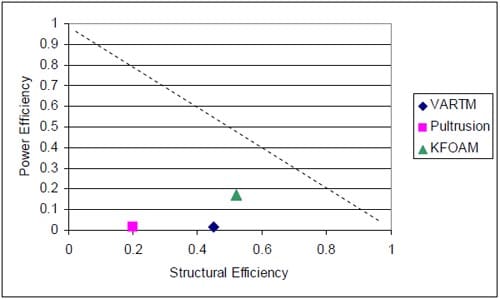
Figure 21. Multifunctional efficiencies of the fuel cell cell designs
4.4 Conclusions
A metric is presented by which the performance of multifunctional fuel cell systems can be characterized. This metric is based on combined measurements of the mechanical and electrochemical behavior of the systems and is designed in order to evaluate a cell’s potential to create system level mass savings. Multifunctional efficiencies ranging from 22% to 69% are attained by the investigated designs. None of the systems enabled system level mass savings, however, the KFOAM based design showed the most promise. This is partly due to the efforts to optimize the structural pressure in this design. Redesigning the systems (1) to reduce electrical losses and (2) with lighter/stiffer materials will allow for improved multifunctional efficiencies. Future work will extend the metric developed here by including the effects of varying mechanical loads on the multifunctional efficiency. The mechanical loads of interest in these cells are the structural pressure load (the pressure in the cell after it is processed and which helps to seal the cell) and the loads which may be applied to the system in its application environment.
Appendix A
An expression for the structural stiffness, S (N/mm), of the multifunctional fuel cell can be obtained using Frostig’s Higher Order Theory. The stiffness can be expressed as the ratio of the concentrated load which is applied at the structure’s top face to the displacement of the structure’s neutral axis. From Equation 9, the total concentrated load is given as
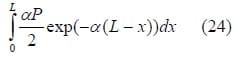
The neutral axis of a sandwich structures subjected to a bending load does not pass through the centroid of the cross section, but is actually displaced toward the tensile face of the beam. From [25], the location of the beam’s neutral axis can be found by
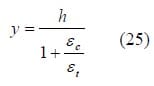
where y = the distance from the midpoint of the bottom face of the beam h = the height of the beam, εc = the compressive strain at the midpoint of the top face, εt = the tensile strain at the midpoint of the bottom face.
Using the Higher Order Theory, it can be shown that the displacement of the beam’s neutral axis, wna, can be accurately approximated by the displacement of the beam’s bottom face, wb. The stiffness of the beam structure can therefore be expressed as
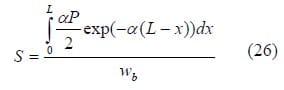
In
terms of the specific (normalized by density) stiffness properties, geometry, and material densities, the stiffness can be rewritten as
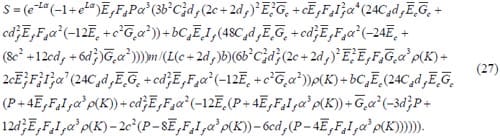
5. Optimization of Polar Plate/GDL Interfacial Contact Pressure for Improved Electrochemical Performance in Multifunctional Fuel Cells
5.1 Abstract
The present study investigates the effects of clamping pressure on the electrochemical performance of multifunctional fuel cell materials. Particular focus was placed on identifying an optimum contact pressure between a conductive foam material, which has been used to replace the polar plates of conventional fuel cells, and the gas diffusion layer (GDL) – as the contact resistance between these cell components is extremely important to the power output of proton exchange membrane fuel cells (PEMFCs). The contact pressures at this interface were examined both numerically and experimentally. These examinations were conducted with the aid of two test rigs: 1) a polycarbonate fixture and 2) a modified fixture in which the polycarbonate components were reinforced by aluminum caps, in order to increase the bending stiffness of the fixture. Electrochemical characterization of the fuel cell materials was accomplished via electrochemical impedance spectroscopy (EIS) and polarization experiments. The resistances at major interfaces in the fuel cell setup were investigated via direct measurement and the application of a fractal model. An optimum pressure of approximate 190 psi, at which the system’s power output exceeded 9 mW/cm2, was found for the system. This power output was likely limited by the high interfacial resistances in the system, as discovered by the contact resistance investigation.
5.2 Introduction
Multifunctional designs are those in which single materials/components perform multiple functions within a system. While the performance of multifunctional devices may be inferior to that of related monofunctional devices, overall system level mass and/or volume savings may be achieved through the incorporation of these designs. The efficient use of material mass/volume may allow for benefits such as cost reductions, reductions in part count, and improved fuel efficiency. The efficiency of many systems which include structural materials, for example ground vehicles used by the U.S. Army and unmanned aerial vehicles, depends on the effective use of energy/power. Structural devices which also possess energy production capabilities, such as multifunctional fuel cells, could therefore aid in the advancement of these Army systems [11, 21].
Clamping pressure has been shown to have great influence on the performance of PEM fuel cells. In particular, this pressure strongly affects the interfacial resistance between the GDL and the polar plate materials. Studies have shown that the resistance at this interface can be quite significant if insufficient clamping pressures are used. This resistance can severely limit the power production abilities of these devices [39-41] . Exponential reductions in this contact resistance have been observed with increasing compression pressures [42]. The pressure with which the fuel cells are assembled will also affect other properties of the fuel cell system. For example, low assembly pressures can lead to leakage of reactants. In contrast, excessive clamping pressures can deform or even damage brittle cell materials such as the gas diffusion layers or thin flow plates. Additionally, increased compression loads may impede reactant transport and water removal due to decreased porosity in the GDL as it is compressed [42, 43]. The variety of effects that assembly pressures may have on fuel cell performance create a need for investigations which attempt to optimize clamping pressure in the PEM fuel cell.
The goal of the current study is to find an optimum clamping pressure for a multifunctional fuel cell. This multifunctional subsystem is designed to provide a larger system with mechanical integrity while producing power and therefore its design deviates somewhat from that of a conventional fuel cell. In particular, the ultimate purpose of the multifunctional cells investigated here is to provide power as well as mechanical support for systems which are subjected to bending loads, and therefore, sandwich structure designs are examined. The study begins with an investigation into the relationship between the applied bolt torque and the contact pressure on the GDL. Next, polarization measurements are taken at various contact pressures to identify an optimum pressure. EIS is then used to observe the effect that pressure has on various fuel cell mechanisms. This is followed by a study of the interfacial resistances (as a function of load) in the cell through direct measurements as well as fractal analysis. Finally, a summary of the mechanisms occurring in the cell is given, based on the determined optimum pressure load.
5.3 Effects of Compression on Fuel Cell
The effects of fuel cell compression in PEMFC systems will now be discussed based on relevant literature. In particular, focus will be placed on the GDL/polar plate interfacial contact resistance and the porosity of the GDL.
5.3.1 Electrical Resistance
Compressive forces are used in PEMFC systems in order to hold cell components together. The amount of compression that is applied to a single fuel cell or a fuel cell stack has a large influence on the electrical characteristics of the cell. The resistance between cell components such as the GDL/bipolar plate (BPP) interface may be very high and create serious potential losses. In fact, some research suggests that approximately 59% of the total power losses in a PEMFC system are due the contact resistance at the GDL/BPP interface [44]. Exponential reductions in this interfacial contact resistance and GDL bulk resistance have been observed with increasing assembly pressure [40, 42]. While some pressure may improve the cell performance, through resistance reductions, excessive pressure may damage brittle components of the cell such as the fibers in the GDL. This will result in increased resistance of the GDL [43]. Therefore, an investigation into the effects of assembly pressure on cell performance is necessary in order to achieve cell optimization.
5.3.1.1 Fractal Model
Majumdar and Tien [45] have modeled the effect of surface roughness on the contact conductance between two surfaces through fractal characterization. While many surface contact models use parameters such as r.m.s. height and mean slope, which vary with the resolution of the measuring instrument, fractal models are based on scale-independent parameters. The fractal model is based on the roughness profiles of two materials in
contact. Many surface profiles, when repeatedly magnified, display similar features under each intensification. It is this behavior which allows characterization through a fractal geometry-based model [46]. The applicability of this model to the prediction of interfacial contact resistance between GDLs and bipolar plates (BPP) materials for fuel cells has been demonstrated by Mishra et al. [47]. The model was shown to be capable of predicting the contact resistance at various GDL/bipolar plate interfaces for many contact pressures with reasonable accuracy. In the current study, the fractal theory is investigated in order to present a mathematical/mechanism-based model which may describe interfacial resistances in the cell as a function of pressure.
Based on a surface profile, z(x) , the roughness of the contacting surfaces may be characterized by a structure function, S(ι) , as
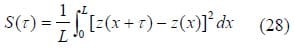
where L is the length of the surface profile. The structure function represents the mean square of the height difference over a special distancet . If the surface profile follows a power law behavior, it is said to be fractal, as
where D is the fractal dimension and G is the scaling constant related to the roughness of the surface. If the profile is indeed fractal, Equation 29 will be displayed as a straight line on a log-log plot. The parameters of this equation correspond to the two surfaces in contact, and must be obtained from a superposition of their structure functions. The fractal parameters, Dand G , are unique to a fractal profile and are independent of the length scale ι. The contact resistance, R , can be expressed as
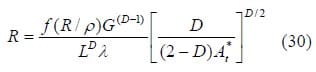
where? is the effective electrical conductivity between the contacting surfaces, A*t is the real area of contact, and ƒ(R/ρ) is a constant which can be found in [45]. The value of A*t depends on the dimensionless load, P* , which is given
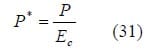
where Ec is the compressive modulus of the gas diffusion layer (for the GDL/BPP interface), as discussed by Mishra [47]. This is a modification to the original model (where hardness was used as the normalizing parameter) which considered contact between two rigid materials.
5.3.2 GDL Permeability
In addition to affecting the resistance in a fuel cell assembly, the pressure applied to the system also determines how easy it is for chemical reactants to access reaction sites (and for reaction products to be removed from the system). Large porosities in the GDL facilitate the diffusion of reactants to the catalyst layer. As pressure is applied to the cell, the porosity of diffusion layer decreases resulting in an increase in its resistance to mass transport [43]. Chang [39] has shown that when a GDL material is compressed by 50% in thickness, its permeability may become 1/10 of the initial value. Ihonen [48] suggested that high clamping pressures increase cell flooding in PEMFC systems and that flooding of the GDL tends to be the dominant source of mass-transfer resistance. In fact, flooding of the electrode, GDL, and flow field has been considered a major technical issue in the development of cost-effective PEMFCs.
5.4 Experimental
5.4.1 Fuel Cell Test Setup
A custom fuel cell testing fixture/setup was used in order to conduct the experimental part of the current investigations (Figure 22). A Nafion 112® MEA with an ELAT® carbon cloth GDL on either side was used for these studies. Catalysts loadings were Pt- Ru of 2 mg/cm2 at the anode and Pt of 4 mg/cm2 at the cathode. The membrane dimensions were 10 cm by 3 cm while the assembly had active electrode dimensions of 9 cm by 2.5 cm. Gasket materials were then placed on either side of the MEA. Previously conducted reactant flow tests showed that optimum leak prevention resulted from a combination of two different gasket materials. This combination included a compressible neoprene/EPDM/SBR rubber foam gasket material (“Gasket 1”) on the anode side of the cell and a silicon gasket material (“Gasket 2”) on the cathode side of the cell. These gasket materials were therefore used in this setup. A strong, lightweight carbon foam material known as KFOAM was then placed on each side of the cell. This foam served as an electrical conductor as well as a reactant distributor for the PEMFC. Stainless steel sheets were then placed along the back side of each carbon foam material. This metallic sheet served as a current collector. Finally, polycarbonate plates which were machined with reactant inlet/outlet ports were bolted together (using 10 bolts) in order to hold the fuel cell components in place. Additionally, a second set of experiments was conducted in which the test fixture was modified. In this setup, aluminum plates were placed outside of the polycarbonate plates for increased stiffness.
5.4.2 Contact Pressure Investigation
5.4.2.1 Finite Element Analysis
3-D models were developed using ANSYS in which SOLID45 and SOLID95 elements were used for the fuel cell setup components (fixture plates, carbon foam, MEA, gasket, and steel sheet). Table 2 contains properties of the assembly components that were used in the models. Additionally, contact pairs which were created using CONTA173 elements along with TARGE170 elements, were used at the GDL/KFOAM interface. Contact pairs were also created at other interfaces within the setup where contact was likely to occur (including between the stainless steel sheet and KFOAM material and along the outer edges of the polycarbonate plates where the plates may touch one another. A rough estimation of bolt forces corresponding to applied bolt torques was obtained using the following equation:
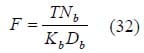
where F is clamping force, T is tightening torque, Nb represents the number of bolts, Kb is the friction coefficient, and Db represents the nominal diameter of the bolts [49]. These forces were used in the FEA models at bolt locations in order to account for the forces applied by the bolts onto the test fixture.
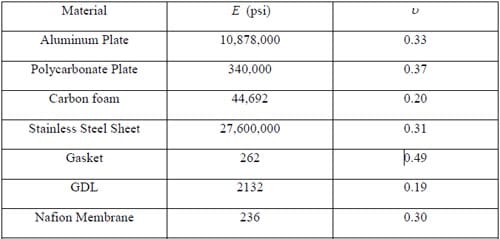
Table 2. Properties used in FEA model of fuel cell assembly
5.4.2.2 Contact Pressure Experiments
In order to determine the contact pressures that existed in the test setup between the KFOAM and the GDL, sheets of PressurexTM, pressure indicating film were placed at this interface on each side of the cell. For the original setup, which included only the polycarbonate plates (as shown in Figure 22), “Super Low” Film (effective between 70- 350 psi) and “Ultra Low” Film (effective from 28-85 psi) were used. The contact pressures were measured at bolt torques ranging from 6 lb·in to 15 lb·in. For the modified fixture, in which aluminum plates were added to the setup, only “Super Low” film was used. Contact pressure experiments for this setup were carried out at bolt torques ranging from 6 lb·in to 16 lb·in.
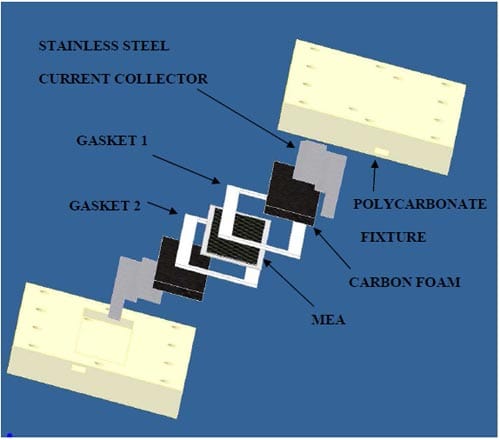
Figure 22. Carbon foam fuel cell design test setup
5.4.3 Electrochemical Characterization
Polarization testing was conducted on a test station manufactured by Fuel Cell Technologies. All tests were conducted at room temperature using a 2 M methanol solution as fuel. A peristaltic pump (Gilson, Minipuls 3) was used to supply the solution to the cell at flow rate of 2 mL/min. Humidified air was fed to the cell cathode at a flow rate of 500 SCCM. No backpressure was applied to the cathode gas. I-V polarization curves were obtained using the two testing fixture configurations mentioned above. Bolt torques from 6 lb·in to 15 lb·in were used for the unmodified fixture, and torques between 8 lb·in and 18 lb·in were applied in the modified test fixture.
Electrochemical impedance spectroscopy experiments were conducted via a Solartron 1252A Frequency Response Analyzer alongside a Solartron 1480 Multistat. These tests were only conducted in the mo
dified test fixture, and the torques used were the same as those used in the polarization studies (8 lb·in-18 lb·in) Impedance spectra were obtained at frequencies ranging from 10000 Hz to 0.025 Hz with measurements recorded at a rate of 10 steps per decade. A sinusoidal voltage signal with a setpoint of 0.25 V and amplitude of 5 mV was applied to the cell during these tests.
5.4.4 Interfacial Contact Resistance Investigation
The contact resistances at the stainless steel/KFOAM interface and the KFOAM/GDL interface were investigated through (1) direct measurement and (2) modeling techniques. In order to measure the resistance at the stainless steel/KFOAM interface, a special test setup was designed. In this setup, a 0.3095”-thick carbon foam section was sandwiched between 2 stainless steel current collector sheets. The resistance through this assembly was then measured with a KEITHLY 2000 multimeter. Measurements were taken at bolt torques ranging from 6 lb·in to 18 lb·in. The total resistance through this setup may be given as
where Rss/kfoam is the interfacial resistance between the stainless steel current collector and the KFOAM, and Rkfoam represents the bulk density of the KFOAM section (which can be calculated based on the material’s resistivity). In a second setup, a GDL was placed at the center of the cell. The GDL was sandwiched between carbon foam materials, and stainless steel sheets were placed outside of the foam sections. The total resistance through this setup may be expressed as
where Rkfoam/gdl represents the contact resistance at the KFOAM/GDL interface and Rgdl represents the bulk resistance of the GDL material, which is given by
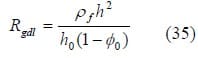
In this equation, ρƒ is the transverse resistivity of the carbon fibers in the GDL, h is the compressed thickness of the GDL, h0 is the initial GDL thickness, and Φ0 is the porosity of the uncompressed material. GDL properties such as thickness and modulus, at various pressures, were calculated based on the compression tests performed by Escribano on ELAT®DSa GDL in [50].
A Hirox Digital Microscope (KH-7700) was used to obtain surface profiles of the stainless steel, KFOAM, and GDL materials. Since the GDL behaves in a nonlinear manner, surface profiles of this component were taken immediately after the material had been subjected to three bolt torques: 10, 12, and 14 lb·in. Surface profiles were then used in order to determine interfacial resistances according to the fractal model procedure in Section 5.3.1.1. The average of four surface scans, each of approximately 16000 microns (630E-3 inches) in length, was used to obtain a structure function representation for each material investigated. In the absence of a hardness value for the KFOAM material, Ekfoam was used in the dimensionless load equation (Equation 31) for the analysis of the stainless steel/KFOAM interface.
5.5 Results and Discussion
5.5.1 Contact Pressure Studies
Pressure distribution results obtained from the ANSYS contact pressure analyses are shown in Fig. 23. The pressure distributions shown correspond to applied bolt torques of 8 lb·in. As expected, the pressures experienced by the GDL in the modified fixture are much more uniform than the pressures on the GDL in the fixture that uses only the polycarbonate end plates. The wide distribution of pressures in the unmodified fixture is due to bending of the polycarbonate plates as torque is applied to the bolts during assembly of the test cell. Lower pressures are observed near the center of the GDL and the pressures tend to increase as the exterior edges (near bolt locations) are approached.
The aluminum plates provide the test fixture with additional stiffness which results in increased uniformity of the GDL contact pressures. Clamping pressure studies have shown that sufficient fixture stiffness/equally distributed pressure is very important in order to achieve optimum fuel cell performance [42, 49, 51, 52], and it has been suggested that uneven distribution of contact pressure may create hot spots that may limit the life of the fuel cell [51]. In FEA studies performed on a fuel cell assembly which included an MEA, sealants, and aluminum endplates, and which was held together by 4 bolts/nuts, Lee et al. [51] observed trends similar to those observed in the current study. Deformation plots on the endplates proved that the deformation at the corners of the plates (where the pressure was applied with the bolts/nuts) was large and that it dropped significantly toward the plates’ centers, creating a nonuniform pressure distribution inside the cell. The authors concluded that the point load assembly technique was ineffective for creating uniform pressure distributions inside the PEM fuel cell.
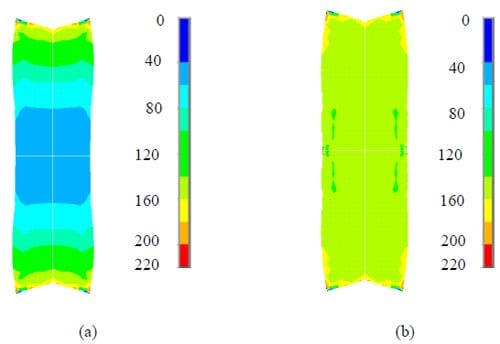
Figure 23. Pressure (psi) distribution on the GDL for an applied bolt torque of 8 lb·in within: (a) fixture with polycarbonate end plates and (b) modified fixture with additional aluminum plates. (Note: Discontinuities at symmetry points likely a result of local bolt loads applied nearby at the symmetry plane)
Figure 24 shows average contact pressures on the cathode GDL in each of the test fixture setups. (Similar results were observed at the anode GDL). Results are included from both the FEA studies and the PressurexTM experimental investigations at applied bolt torques ranging from 6 lb·in to 16 lb·in (from 6 lb·in to 15 lb·in for the unmodified fixture). FEA studies seem to suggest a linear relationship between the bolt torque and the contact pressure that the GDL experiences in both test fixtures while the PressurexTM results seem to vary. While a linear relationship between the two variables is obvious in the unmodified fixture, the nature of the relationship is not as obvious in the modified fixture.
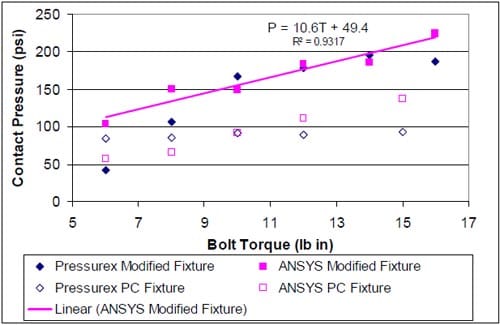
Figure 24. Contact pressures obtained from PressurexTM film studies and from ANSYS for fixture with polycarbonate end plates and modified fixture, with additional aluminum plates
It is obvious that there is a slight lack of agreement between the two techniques in the unmodified fixture, outside of the 10 lb·in bolt torque. Below this bolt torque, ANSYS seems to underestimate that contact pressure, while above this torque, the numerical technique seems to overestimate the contact pressure. This disagreement between the two analysis methods could be due to the difficulty encountered in calculating the average pressures with the unmodified fixture. As previously discussed, this fixture experienced significant bending during cell assembly. This bending created a wide range of pressures on the GDL and necessitated the use of two different pressure sensitive film types (in order to account for the entire pressure range experienced by the GDL). Calculating an average contact pressure from the two films proved to be a challenging task. Figure 24 reflects results obtained by averaging the average pressure from each film. While this is a straightforward approach, it may lead to inaccuracies in the results.
The modified fixture seems to show better agreement between t
he two techniques, particularly at 10 lb·in and above. This may result from the fact that only one type of pressure sensitive film was necessary in this case (due to the stiffened fixture and the resulting uniformity in the contact pressures on the GDL). The differences in the two techniques at the lower torque values may be explained by the unevenness of the carbon foam materials used in the tests. While all carbon foam materials were machined to an approximate thickness of 0.125”, precise measurements showed that the thickness of the materials varied by as much as 0.02” across the sample in some cases. Figure 25 displays an analyzed impression that was created at a bolt torque of 8 lb·in in the modified fixture. It is obvious from the analyzed image that there are regions within the rectangular area (especially near the central portion) where no contact was detected by the film. This is a direct result of the variation in the thickness of the foam at different locations. An increase in the contact area detected by the pressure sensitive film was observed at the elevated torques (10 lb·in-16 lb·in). Considering this reduction in actual contact area (due to uneven foam surfaces) at the lower bolt torques, it may be concluded that the ANSYS model developed can be used to accurately predict the contact pressures experienced by the GDL in the modified fixture for the bolt torques studied here. The relationship between the applied bolt torque and the contact pressure at the GDL/KFOAM interface may therefore be expressed as
where P is the average contact pressure at the interface and T is the applied bolt torque.
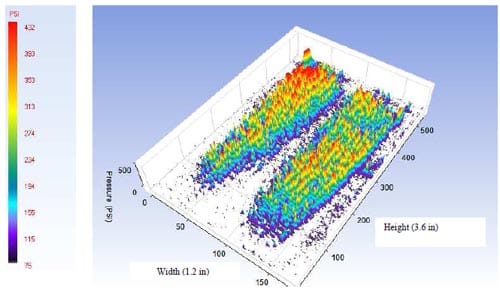
Figure 25. Contact pressure distribution at carbon foam/GDL interface in modified fixture at an applied bolt torque of 8 lb·in
5.5.2 Electrochemical Studies
5.5.2.1 Polarization Studies
Figure 26 displays polarization curves obtained from both test fixtures at various bolt torques. In the unmodified fixture the performance of the fuel cell materials increases with bolt torque throughout the range of torques tested. In the modified fixture, however, there seems to be an optimum bolt torque of 14 lb·in. In this test setup, the performance of the fuel cell materials improves with applied torque from 8 lb·in to 14 lb·in and then begins to decrease. This trend is shown in terms of power output by the fuel cell at various contact pressures (using Equation 36) in Figure 27. This figure shows that the power output by the fuel cell materials increases from just above 4 mW/cm2 to above 9 mW/cm2 between contact pressures of 134 psi and 198 psi. The performance then begins to decrease, approaching nearly 7 mW/cm2 at 240 psi. Possible reasons for this behavior will be discussed below.
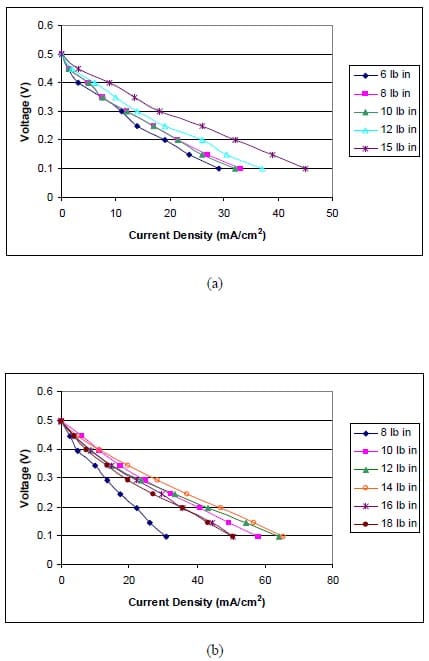
Figure 26. Polarization curves at various bolt torques in: (a) polycarbonate fixture and (b) modified fixture
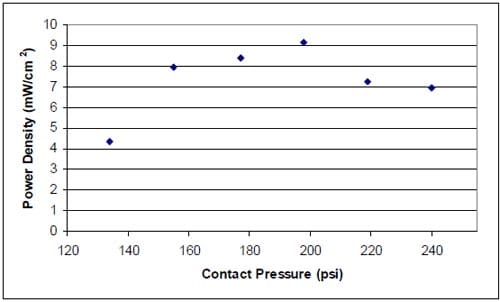
Figure 27. Power output by fuel cell materials in modified fixture at various contact pressures
5.5.2.2 Electrochemical Impedance Spectroscopy Studies
Electrochemical impedance spectra obtained in the modified fixture are displayed in terms of the applied bolt torques in Figure 28 (lb·in = “pi”), and internal resistances in terms of the contact pressures on the GDL (from Equation 36) are shown in Figure 29. The locations where the spectra (Figure 28) intersect the axis corresponding to the real part of the impedance (the horizontal axis) at high frequencies represent the internal resistance values of the cells [53] while x-intercepts at lower frequencies (higher Re Z values) give information on the reaction kinetics of the electrochemical interface [54]. The diameter (the distance between the two intercepts) of the curves is representative of the total activation resistance of the cell. In general, outside of the lowest applied torque (8 lb·in), no trend is obvious between the diameter of the curves and the applied bolt torque – as the diameter remains fairly constant. This behavior is different from that observed in previous work such as the investigation conducted by Ihonen et al. [48] where higher compression forces led to increased mass-transfer resistances (due to loss of porosity in the GDL), which resulted in curves of increasing diameter. This may indicate that the foam material, and not the GDL, is dominant in controlling the mass transfer characteristics of the cell assembly.
It can be observed in both figures that the internal resistance tends to decrease as the torque applied to the test setup increases. This trend in the internal resistance may explain the electrochemical behavior of the cell in observed in Figures 26 and 27. Higher bolt torques may allow for improvements in the overall electrical conductivity of the GDL along with decreased contact resistances between cell components, and therefore, minimize cell losses due to electrical resistance [55].
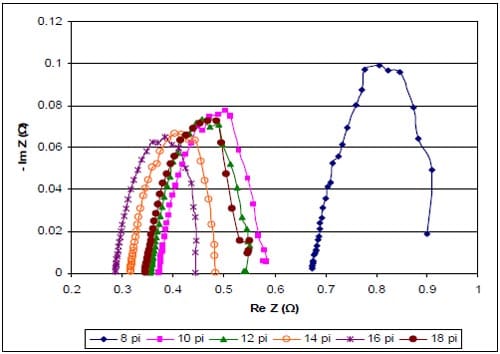
Figure 28. Nyquist plots obtained in modified fixture at various bolt torques
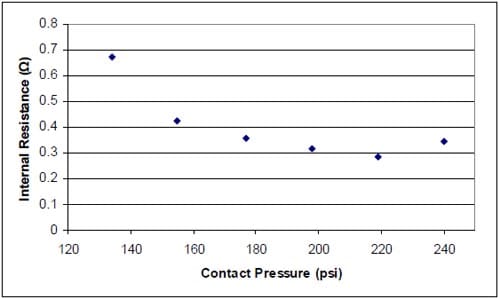
Figure 29. Internal resistance through fuel cell in modified fixture at various contact pressures
An initial, rapid decrease in the cell’s internal resistance is observed between the GDL and KFOAM material as the contact pressures begin to increase. This decrease likely plays a large role in the increase of the power output by the cell in the corresponding torque range. Beyond 200 psi, decreases in the cell’s internal resistance are minimal. This initial, quick decrease in resistance with increasing contact pressure followed by minimal resistance changes as contact pressure continues to increase is similar to the behavior observed at the bipolar plate/GDL interface by Zhang et al. [40]. Similar resistance/clamping pressure relationships have also been observed by Mishra et al. [47]. The decrease in contact resistance with increasing contact pressure is due to increases in the actual contact area between the asperity structures at the interface. Above 220 psi, a slight increase is observed in the internal resistance of the cell. This increase may be a result of the initiation of damage to brittle cell components, such as the GDL, due to excessive pressures [42, 43]. Subsequent EIS measurements seemed to confirm this claim as general increases in the internal resistance were observed relative to the points shown in Figure 29. General behavior agreement is observed between the power output curves and the cell resistances obtained from the EIS measurements, indicating that cell resistance may be the largest influencing factor on the power output by this fuel cell assembly.
5.5.3 Contact Resistance Investigation
The interfacial resistances calculated from the contact pressure investigation (using Equations 30, 33, and 34) are shown in Table 3. The resistances are given as a function of pressure, where the contact pressures of 145 psi, 181 psi, and 186 psi correspond to the applied bolt torques of 10 lb·in, 12 lb·in, and 14 lb·in, respectively.
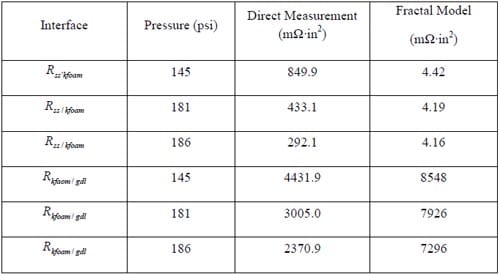
Table 3. Contact resistances obtained through direct measurement and fractal analysis
T
here is a lack of agreement between the resistance measurements obtained through the fractal model and those obtained from direct measurement. The fractal model values are below the direct measurement values at the stainless steel/KFOAM interface and above the measured values at the KFOAM/GDL interface. Currently, the reason for this difference is not clearly understood. It may be related to the modifications used in order to adapt the model to the current situation or it could be necessary to perform more surfaces scans in order to get a better representation of the material surface profiles. Obtaining surface scans from another instrument (such as a profilometer) on the stainless steel sheet could be used to validate the potential of the digital microscope for surface studies. This issue will be investigated in the future. In general, the contact resistances observed in Table 3 are higher than those found in the literature at BPP/GDL interfaces. Mishra et al. [47] observed interfacial contact resistances ranging from 0.155 mΩ·in2 to 1.6 mΩ·in2 for the various GDL/BPP contacts that he investigated. The high resistances are likely due to the roughnesses of the surfaces involved in this study, particularly the KFOAM material. Mishra observed values ranging from 440 µin to 790 µin for the fractal parameter G . The G parameter values (which are representative of asperity heights) obtained in the current study are near 2E25 µin for the stainless steel/KFOAM interface and approximately 1.13E53 for the KFOAM/GDL interface. The surface of the carbon foam material can be seen in Figures 30 and 31. The surface roughness of the KFOAM likely creates only isolated contact spots at these interfaces. This roughness of the surfaces involved in the fuel cell assembly likely limit the power output potential of the cell. This study demonstrates the importance of considering the surface roughness of the cell components when designing a multifunctional fuel cell.
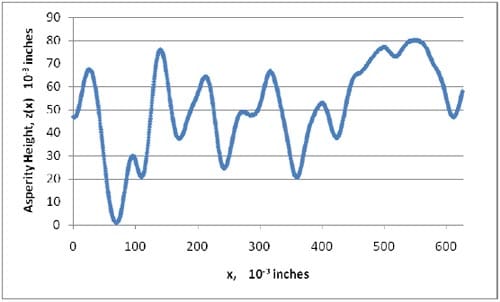
Figure 30. Surface profile obtained from KFOAM sample
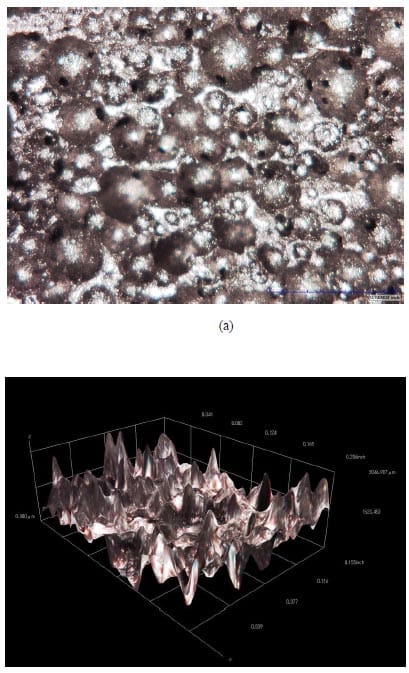
Figure 31. (a) Image showing surface of KFOAM section and (b) topography of KFOAM
5.6 Conclusions
Contact pressure significantly affects the ohmic and mass-transport properties of a fuel cell system. Every fuel cell configuration has an optimum pressure at which it may achieve its peak performance. An optimum pressure of about 190 psi was found for the multifunctional fuel cell system investigated in this study. The merits of a uniform pressure distribution were demonstrated by improvement in the overall cell performance of the system with a stiffer test fixture. For the modified test fixture investigated in the current study, the electrical resistance seems to be the dominant mechanism influencing the power output by the device. No significant changes in mass transfer properties are observed as pressures on the assembly are varied. Interfacial resistances calculated from the fractal model are very different from the values calculated through direct measurements. The cause of this difference is not clearly understood at this point, and future efforts will attempt to address this issue. The performance of the fuel cell is likely limited by the roughness of the surfaces involved, particularly the KFOAM material. The power output by the system could therefore be improved by incorporating a smoother plate material and/or reducing the number of interfaces. Ultimately, the results of the current study will be used to aid in the design of efficient multifunctional fuel cells.
6. Analysis of a Multifunctional Fuel Cell Design through Simultaneous Bending and Electrochemical Testing
6.1 Abstract
In order to obtain a reliable prediction of how a multifunctional structure will perform in an actual application environment, it is important to examine the desired functions of the structure/system simultaneously. In particular, the multifunctional fuel cells of interest here are required to provide power for a system while undergoing mechanical bending loads. For this reason, analyzing the electrical and mechanical performances of the structure independently may not provide an accurate indication of the multifunctional efficiency of the device. In the current study, electrochemical measurements (EIS and polarization) were performed on a simulated multifunctional fuel cell while it was subjected to concentrated 3-point bending loads in order to observe the influence that the mechanical loads may have on the electrochemical performance of the device. Finite element analyses were conducted in order to estimate the stress distributions (at the fuel cell’s midplane – the location of the MEA) which resulted from the mechanical loads. This study demonstrates the influence of two pressure loads, the inherent structural pressure and the concentrated bending load, on the electrochemical performance of a structural fuel cell assembly. As pressure is known to affect various mechanisms in a fuel cell system, both loads should be accounted for in the design an efficient multifunctional fuel cell.
6.2 Introduction
Multifunctional material systems and structures are capable of performing two or more distinct functions. These functions may be mechanical, chemical, or electrical in nature and may be executed simultaneously or sequentially. The ultimate goal of multifunctional designs is to achieve system level improvements, such as reductions in system weight or volume, with less concern for obtaining optimal functional performance from separate subsystems [6, 14]. In applications such as spacecraft, reductions in system weight can lead to savings in launch costs [4, 56]. Additionally, multifunctional design integration may allow for reductions in part count and installation effort [37].
Multifunctional systems which combine structural integrity with energy storage/generation functionalities have been investigated by researchers with the U.S. Army and researchers from the U.S. Navy. Both organizations have made progress with structural batteries efforts [6, 11, 13, 14, 16]. These multifunctional systems are capable of providing power for a system while supporting mechanical loads. The U.S. Army has also examined the use of composite materials in order to create multifunctional capacitors [8, 11, 23] and multifunctional fuel cells [11, 21] . The multifunctional capacitors and fuel cells are designed to carry mechanical loads while storing energy and producing power, respectively.
Various manufacturing techniques have been successfully used in order to create multifunctional fuel cell structures [11, 21, 37]. These multifunctional fuel cells rely on the inherent structure to provide the pressure which holds the cell components in place/together. Changes in this pressure will result in changes in the power output by the device, as it is well known that the pressures on a fuel cell’s GDLs play a significant role in the efficiency of the device [39, 40, 42, 57]. For the multifunctional fuel cells, the intensity of this pressure depends on material/processing details, and it will vary as mechanical loads are applied to the device. This structural pressure is responsible for ensuring adequate contact to minimize interfacial resistances between cell components, such as the bipolar plates and the GDLs and helping to seal the cell in order to avoid reactant leaks. The level of pressure must, however, be low enough as to avoid impeding the transport of reactants and by-products, by over compressing the GDL, as this will increase the resistance to flow.
Lee et al. [55] conducted an investigation on the compression pressure (on the GDL) in PEM fu
el cell assembly in order to determine the pressure at which an optimal balance of these effects occurred. The authors investigated three types of commercially available gas diffusion layers (TORAY®, ELAT®, and CARBEL®) of varying thicknesses at three different assembly bolt torques (100 lb·in, 125 lb·in, and 150 lb·in). For the ELAT® gasket, a porous and compressible material, the authors discovered an optimum compression pressure occurred at 125 lb·in. This pressure resulted in enhanced electrical contact, but further compression created mass transfer resistances and reduced performance. The TORAY® gasket, a brittle material, displayed a decrease in performance as the pressures increased. Additionally, the power densities achieved from this gasket were less than those obtained by the ELAT® gasket. The poor performance of this gasket was attributed to damage of the GDL layer, resulting in high resistances between the GDL and the flow plates. A third test, of a hybrid CARBEL®-TORAY® gasket combination, showed an optimum pressure at 125 lb·in. Bazylak et al. [58] used scanning electron microscopy to examine TORAY® non-woven fibrous gas diffusion layers after they were subjected to pressures between 26 psi and 200 psi. Damage was seen at all pressures, but its severity increased with pressure. Ge et al. [59] studied the effects that compression had on GDL materials via polarization measurements at various compression ratios. The results of the study showed that generally, fuel cell performance initially increases with increasing compression, and then decreases after reaching a certain level of compression. The authors concluded that there is an optimal compression ratio at which the performance of a fuel cell system is maximized and that GDL compression should be carefully controlled in order to reach this point.
Therefore, in order to optimize a multifunctional fuel cell’s power output, it is imperative that attention is given to the mechanical pressures applied perpendicular to the GDLs, MEA, and collector plate assembly. The aim of the current investigation is to initiate an understanding of the influence that mechanical bending loads may have on the electrochemical performance of multifunctional fuel cell structures.
6.3 Experimental
6.3.1 Fuel Cell Assembly
A multifunctional fuel cell design (Figure 32) which contained a custom MEA along with conductive carbon foam reactant distribution media and 0.01-inch stainless steel current collector plates was analyzed in the study. The dimensions of the carbon foam sections were 3.5 inches, 0.16 inches, and 1 inch for the length, width, and thickness, respectively.
The MEA was composed of a Nafion 112® membrane with a carbon cloth GDL on either side. Catalysts loadings of Pt-Ru at 2 mg/cm2 and Pt at 4 mg/cm2 were used on the cell’s anode and cathode sides, respectively. A compressible neoprene/EPDM/SBR rubber foam materials was used as a gasket on the anode side of the cell while a silicon material was used on the cathode side of the cell. A custom Lexan fixture was used to house the fuel cell components during the investigation. 0.5-inch thick polycarbonate plates were machined to length and width dimensions of 5 inches and 3.35 inches, respectively, for the assembly. The cell components were held together using 10 bolts. For the current study, the bolt holes were slotted to allow for sliding (shearing) in the assembly during the mechanical loads. Four stainless steel washers were used with each bolt (two on each side of the cell) at in an attempt to enhance the setup’s potential for sliding. Two additional holes were placed in each polycarbonate plate and used as inlet and outlet locations for the reactants.
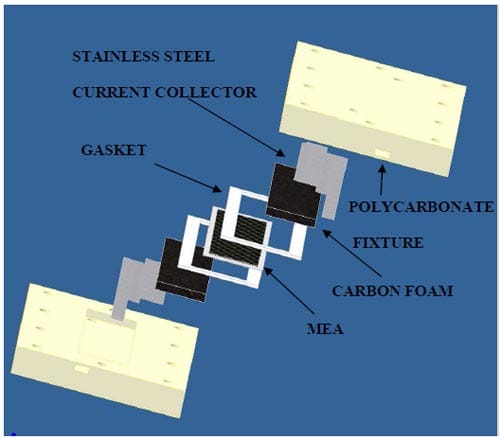
Figure 32. Fuel cell assembly
6.3.2 Test Setup
A custom setup (Figure 33) was used to load the fuel cell assembly in 3 point bending. The assembly was placed onto an adjustable fixture which supported the ends of the bottom polycarbonate plate. The fixture was set at a span of nearly 5 inches to match the length of the polycarbonate plate. A 0.25” diameter steel rod was placed along the center of the upper Lexan plate. High strength nylon string was then tied to each end of the rod, creating a loop. A hanger was hooked onto the bottom of the nylon loop and free weights were placed on the hanger in order to apply the concentrated load, F. Loads ranging from 0 pounds to 80 pounds were applied to the assembly, in 20-pound increments. (The weights of the steel bar and the hanger were considered relatively insignificant and were not included in load calculations). Additionally, three assembly bolt torques were investigated in the current study – 3 lb·in, 5 lb·in, and 7 lb·in. Bolt torques below 3 lb·in were unable to provide sufficient pressure to seal the multifunctional.
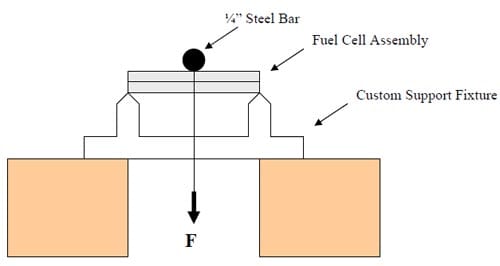
Figure 33. 3-point bending test setup for fuel cell assembly
The maximum displacement reached at each loading condition was obtained using an INSTRON 5500R test station. A 225-lb load cell was used along with a ¼-in load nose, and experiments were conducted at a strain rate of 0.01 in/min.
6.3.3 Electrochemical Characterization
Polarization experiments were conducted on a test station manufactured by Fuel Cell Technologies. All tests were performed at room temperature. Additional testing conditions included an air flow rate of 500 SCCM to the cell’s cathode and an anode fuel flow rate of 2 mL/min. A 2 M methanol solution was used as the anode fuel, and it was supplied to the cell with the aid of an external peristaltic pump (Gilson, Minipuls 3).
Additional electrochemical characterization was accomplished via electrochemical impedance spectroscopy (EIS). A Solartron 1252A Frequency Response Analyzer and a Solartron 1480 Multistat were used for the EIS experiments. A sinusoidal voltage which was set at 0.25 V with an amplitude of 5 mV was used for these experiments. Impedance spectra were recorded at frequencies ranging from 10000 Hz to 0.03 Hz at 10 steps per decade.
6.3.4 Finite Element Analysis
A 3-dimensional, simplified model of the fuel cell assembly was created in ANSYS. Solid 45 elements were used to mesh the model’s volumes, such as the washers, Lexan plates, etc. In this simplified model, the electrical fuel cell components (MEA, KFOAM, and stainless steel) were modeled as one homogeneous structure, the properties of which were obtained in a separate ANSYS analysis. In the separate analysis, normal (compressive) and shear loads were applied to an assembly consisting of the electrical fuel cell components in order to observe the resulting displacements. Linear elastic behavior was assumed and the effective elastic parameter inputs for the homogeneous fuel cell structure were obtained. The properties used for the cell components are give in Table 4. Contact pairs (using CONTA 173 and TARGE 170 elements) were placed at locations in the model where contact was likely to occur, such as between the Lexan and homogeneous fuel cell structure as well as along the outer edges of the polycarbonate plates, where the plates may touch each other as the fixture is tightened. Pressures were applied to the face of the washers as well as to a thin area (approximating a line) across the center of the upper Lexan plate to account for the bolt loads and the concentrated load, respectively. The integrity of the mesh was verified as negligible changes in results were observed with refined meshing.
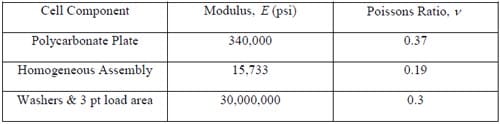
Table 4. Properties of materials used in ANSYS model
6.4 Results and Discussion
6.4.1 Electrochemical Analysis
Polarization curves obtained from the fuel cell assembly at a bolt torque of 3 lb·in and various bending loads are shown in Figure 34. A general trend is evident in which the performance of the fuel cell is reduced as the bending load is increased. Similar behavior was observed at the other bolt torques, 5 lb·in and 7 lb·in, as well. The slope of the polarization curves in the ohmic region can be seen to decrease with increasing bending loads, indication an increase in the electrical resistance through the assembly. The maximum power density obtained at each mechanical loading condition is presented in Figure 35. The power output by the cell is much lower than should be expected from a Direct Methanol Fuel Cell operating under similar conditions, and it decreases as the concentrated bending load increases (for each bolt torque tested). Additionally, there is a reduction in the power achieved by the assembly as the bolt torque is increased between 3 lb·in and 7 lb·in.
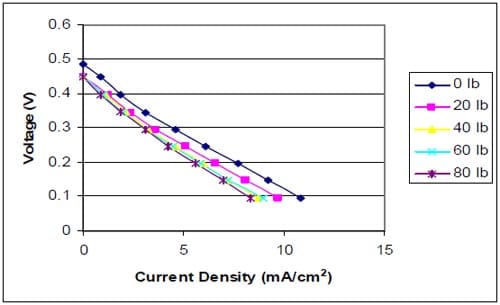
Figure 34. Polarization curves for fuel cell assembly at various concentrated bending loads and a bolt torque of 3 lb·in
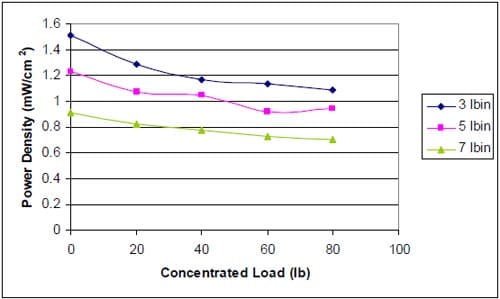
Figure 35. Maximum power density achieved in the fuel cell assembly for each bolt torque at various concentrated bending loads
Nyquist plots obtained from the EIS studies at a bolt torque of 3 lb·in are displayed in Figure 36. The plot shows a general increase in the resistance through the cell (the location where the semicircle crosses the real impedance axis) as higher bending loads are applied to the assembly. Additionally, the real impedance values are higher than should be expected from the cell, even for the condition of no bending load. This may indicate that contact between cell components is poor or that it is excessive and may be causing damage of brittle cell components.
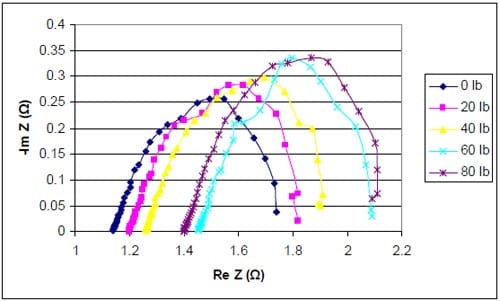
Figure 36. EIS spectra for fuel cell assembly at various concentrated bending loads and a bolt torque of 3 lb·in
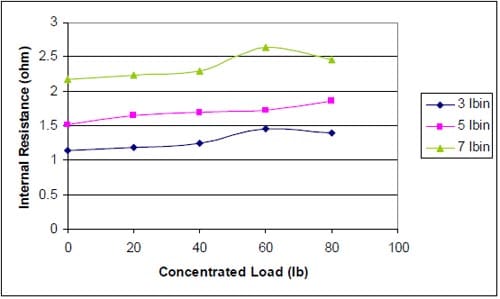
Figure 37. Summary of internal resistance values measured from fuel cell assembly
6.4.2 Finite Element Analysis
Stress distributions obtained from the FEA studies are displayed in Figure 38. The figure presents compressive stresses and shear stresses at the fuel cell assembly’s midplane for a bolt torque of 3 lb·in and a 40 lb bending load. The plot displays a wide range of compressive stresses resulting from this loading condition – from 33 psi near the central area to 804 psi near the outermost edge. A similar, uneven distribution of compressive stress was observed in the numerical model of Lee et al. [51] as well. The authors investigated a single PEM fuel cell which was assembled with 4 bolts through aluminum endplates. The FEA model showed significant bending in the endplates during cell assembly, and the researchers concluded that the point load method is ineffective for achieving a uniform distribution of compressive pressure in a fuel cell. An even pressure distribution is important in order to achieve optimum performance from PEM fuel cells [52], and a pressure between 215 and 290 psi is usually required to reach minimal contact resistances [49]. Figure 38(a) shows that most of the compressive pressures are outside of this range. Near the center of the cell, the compressive stresses are below this range. This is likely due to bending of the polycarbonate fixture which results in poor contact between the GDL and the KFOAM material in this area. On the other hand, the stresses are much higher near the outer regions of the cell. These stresses may damage brittle cells components such as the GDL fibers and catalysts layers. Large areas outside of the optimum pressure range may therefore be responsible for the elevated resistances evident in the EIS spectra (Figures 36 and 37). Figure 39 displays the average areal compressive pressure at each loading condition. In general, the compressive pressures observed in the FEA investigation are seen to increase 1) as increasing bending loads are applied at a particular bolt torque and 2) as the bolt torques increase between 3 lb·in and 7 lb·in. This may explain the general increase in semicircle diameter with increasing bending load observed in Figure 36. This increase in diameter has been attributed to increases in masstransfer resistance [48] as excessive pressures on the GDL lead to compression of the material and losses in its porosity. Additionally, these pressures may be causing damage to the catalysts layers of the MEA, leading to large activation losses in the cell. Figure 40 shows the maximum deflections obtained at each mechanical loading condition from the experimental and numerical studies. As expected, increased deflections are evident as the concentrated load is increased. Additionally, increased bolt torques generally result in reduced deflections. The differences between the two techniques are very small. In general, the difference in deflections is approximately 0.003 inches at a concentrated load of 20 lb and approximately 0.009 inches at a 40 lb concentrated load, for all bolt torques considered. This agreement between the techniques helps to validate the integrity of the ANSYS model used.
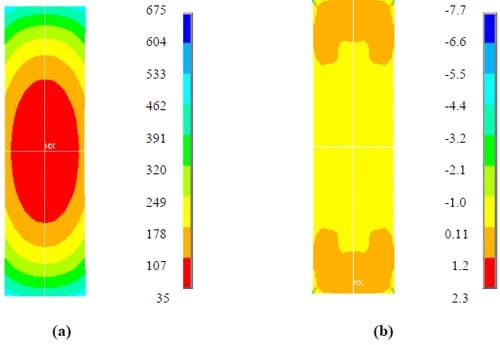
Figure 38. 3 lb·in bolt torque and 40 lb bending load: (a) Transverse compressive stress (psi) distribution at the fuel cell’s midplane and (b) shear stress (psi) distribution at the fuel cell’s midplane
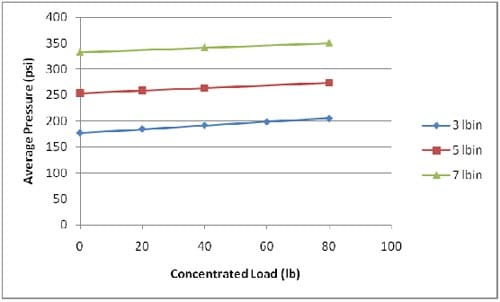
Figure 39. Area-based average compressive pressure at each loading condition
Although the simulated fuel cell assembly was designed in order to allow for shear/sliding during application of the bending loads, negligible sliding was observed in the experimental test fixture. The magnitudes of the shear stresses obtained from the ANSYS studies are also small (as evident in Figure 38(b)). The limited shear in the fixture was likely a result of the high normal, compressive loads applied at the bolt locations. Future FEA models will incorporate the interfaces formed by the different cell components, such as the GDL, the carbon foam, and the stainless steel current collector, in order to more accurately determine the shear stresses within the system when it is subjected to bending loads.
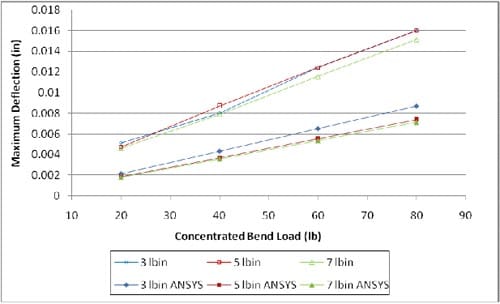
Figure 40. Maximum deflections obtained through experimental and numerical investigations
6.5 Conclusions
The importance of simultaneous consideration of functions in a multifunctional device is demonstrated. Though the power outputs in the current investigation are low, it is evident that mechanical loads significantly affect the power output by the multifunctional fuel cell. This is because the pressures on the fuel cell significantly affect cell properties such as ohmic and mass transport resistances. The results show that bending loads tend to increase the overall pressure at a fuel cells midplane. In a multifunctional cell, this bending load will add to the inherent structural pressure. In order to optimize the multifunctional fuel cell, consider
ation of the load that the cell may be subjected to should be used in designing/manufacturing the cell. It is recommended that the multifunctional fuel cell be designed so that the majority of the contact pressure comes from the inherent structural load, and that the effects of other loads, such as bending loads (which may disrupt the uniformity of pressure distribution) be minimized.
7. Summary of Conclusions/Future Work
This dissertation has investigated/discussed the development of multifunctional fuel cell structures, characterization of the cells, optimization of cell performance, and the influence that mechanical loads may have on the cells.
The first section reviewed novel fuel cell architectures and presented another design. The review showed that VARTM and pultrusion were effective techniques in the processing of these multifunctional structures. Additionally, a multifunctional metric was developed and applied to three cell designs. Multifunctional efficiencies ranging from 22% to 69% were achieved by the investigated cell designs. While these efficiencies fall short of the mark for system level mass savings, this study showed the importance of operating parameters, particularly, cell assembly pressure, on the performance of the multifunctional systems. The transverse pressures applied to the fuel cell structural cell must be considered in order to achieve a design of significant multifunctional efficiency. Future work will include an extension of the metric to include the influence of mechanical pressures on the electrochemical performance of the devices, once more quantitative investigations are performed in the area. The inclusion of the mechanical pressures on electrochemical performance is very important for accurate efficiency predictions, as has been illustrated in the second and third articles within this dissertation. Additionally, exploration of alternative (structural and electrical) materials should continue in order to reach system level mass savings.
The second portion of the document investigated the effect of assembly pressure on a multifunctional fuel cell design. Pressure was shown to significantly impact the electrochemical performance of the device. An optimum pressure of approximately 190 psi was identified for the investigated model design. This pressure corresponded to minimal resistances in the cell. Optimum pressure values will be used to guide the design/processing conditions of future cells in order to achieve efficient multifunctional systems. Interfacial contact resistances calculated through measurements did not agree with results obtained with fractal analysis. It is recommended that reasons this discrepancy be explored. An increased number of surface profiles from each material may provide a more accurate representation of each surface. Additionally, profile measurements can be made with another instrument in order to validate those obtained from the Hirox digital microscope. It is also recommended that alternatives to the carbon foam material be investigated in order to reduce interfacial resistance losses in the cell. Optimization of other parameters such as fuel flow rate, air flow, rate, methanol concentration, should also be considered.
The final section explored the effects of mechanical loads (inherent, structural compression and applied bending loads) on the electrochemical performance of the cells. The influence of the loads was shown to be significant. For the model cell investigated, increased pressure resulted in decreased performance. The effect of pressure on ohmic and mass transport within the system should be considered when designing a multifunctional cell. It is recommended that multifunctional cells be designed so that the internal, structural pressure is the dominant load, so that deformation from external, applied loads is minimized. FEA studies of potential designs and loading situations may be invaluable in this effort. Additionally, attempts should be made to understand the effects of processing parameters on internal, structural pressures – for example, foam dimensions are very important in the pultruded cell design (as this foam material is forced through a die of set dimensions) as they dictate the internal pressure on the fuel cell materials.
The development of a multifunctional fuel cell design has been shown to be an achievable task, through processes such as VARTM and pultrusion. The electrochemical performance of the cell is highly dependent on the transverse mechanical pressure applied to the fuel cell components. Therefore, in order to attain a structural fuel cell with a favorable multifunctional efficiency, consideration should be given to the loads applied to the fuel cell (both the structural load which results from processing and the loads which the fuel cell is subjected to in its operation environment), as well as the materials used in the design.
References
- Thomas, J.P., and M. A. Qidwai, Mechanical Design and Performance of Composite Multifunctional Materials. Acta Materialia, 2004. 52: p. 2155-2164.
- Wetzel, E.D., Reducing Weight: Multifunctional Composites Integrate Power, Communications, and Structure, in Amtiac Quarterly. 2004.
- Torquato, S., Hyun, S., and A. Donev, Optimal Design of Manufacturable Three- Dimensional Composites with Multifunctional Characteristics. Journal of Applied Physics, 2003. 94(9): p. 5748-5755.
- Guerrero, J., Fosness, E.R., and K. Qassim. Overview of Multifunctional Structure Efforts at the Air Force Research Laboratory. in Space 2000: The Seventh International Conference and Exposition on Engineering, Construction, Operations, and Business in Space. 2000. Albuquerque, New Mexico.
- Torquato, S., Hyun, S., and A. Donev, Multifunctional Composites: Optimizing Microstructures for Simultaneous Transport of Heat and Electricity. Physical Review Letters, 2002. 89(26): p. 266601-1-266601-4.
- Snyder, J., Carter, R., and E. Wetzel, Electrochemical and Mechanical Behavior in Mechanically Robust Solid Polymer Electrolytes for Use in Multifunctional Structural Batteries. Chemistry of Materials, 2007. 19(15): p. 3793-3801.
- Rawal, S., Barnett, D.M., and D.E. Martin, Thermal Management for Multifunctional Structures. IEEE Transactions on Advanced Packaging, 1999. 22(3): p. 379-383.
- O’Brien, D.J., Baechle, D.M., and E.D. Wetzel. Multifunctional Structural Composite Capacitors for US Army Applications. in International SAMPE Technical Conference. 2006.
- Baucom, J.N., Pogue III, W.R., Thomas, J.P., and M.A.Qidwai. Hydrocarbon Fuels as Multifunctional Structure-Power for Unmanned Air Vehicles. in 3rd International Energy Conversion Engineering Conference. 2005.
- Barnett, D.M., and S. Rawal, Multifunctional Structures Technology Experiment on Deep Space 1 Mission. IEEE AES Systems Magazine, 1999.
- South, J., Baechle, D., Hilton, C., O’Brien, D., and E. Wetzel, Multifunctional Power-Generating and Energy Storing Structural Composites for U.S. Army Applications. Materials Research Society Symposium Proceedings, 2005. 851: p. 139-150.
- Polymer Composites Have Tunable Electromagnetics/Multifunctional Batteries Build Vehicle Structures. Advanced Materials and Processes, 2004.
- Thomas, J.P., Qidwai, M.A., Matic, P., Everett, R.K., Gozdz, A.S., Keennon, M.T., and J.M. Grasmeyer. Structure-Power Multifunctional Materials for UAVs. in Proceedings of SPIE – The International Society for Optical Engineering. 2002.
- Qidwai, M.A., Thomas, J.P., and P. Matic. Structure-Battery Multifunctional Composite Design. in Proceedings of SPIE. 2002.
- Qidwai, M.A., Baucom, J.N., Thomas, J.P., and D.M. Horner, Multifunctional Applications of Thin Film Li Polymer Battery Cells. Materials Science Forum, 2005. 492: p. 157-162.
- Thomas, J.P., and M.A. Qidwai, The Design and Applic
ation of Multifunctional Structure-Battery Materials Systems. JOM, 2005. 57(3): p. 18-24. - Ilic, D., Holl, K., Birke, P., Wohrle, T., Birke-Salam, F., Perner, A., and P. Haug, Fuel cells and batteries: Competition or separate paths? Journal of Power Sources, 2006. 155: p. 72-76.
- Deluca, N.W., and Y.A. Elabd, Polymer Electrolyte Membranes for the Direct Methanol Fuel Cell: A Review. Journal of Polymer Science: Part B, Polymer Physics, 2006. 44: p. 2201-2225.
- Vaidya, U.K., Multi-Functional Sandwich Composites. Smart Materials, Structures, and Systems, Proceedings of SPIE, 2003. 5062: p. 621-628.
- South, J.T., Campbell, J., Wetzel, E.D., and S.M. Walsh. Multifunctional Composite Direct Methanol Fuel Cell. in First International Conference on Fuel Cell Development and Deployment. 2004. UCONN.
- South, J., Baechle, D., Hilton, C., DeSchepper, D., and E. Wetzel, Design and Response of a Structural Multifunctional Fuel Cell. 2008, Army Research Lab: Aberdeen Proving Ground.
- Kaempgen, M., Lebert, M., Roth, S., Soehn, M., and N. Nicoloso, Fuel Cells Based on Multifunctional Carbon Nanotube Networks. Journal of Power Sources, 2008. 180: p. 755-759.
- Baechle, D.M., O’Brien, D.J., and E.D. Wetzel. Design and processing of structural composite capacitors. in International SAMPE Symposium and Exhibition. 2007. Baltimore: Soc. for the Advancement of Material and Process Engineering.
- Dai, J., and H. Thomas Hahn, Flexural Behavior of Sandwich Beams Fabricated by Vacuum-Assisted Resin Transfer Molding. Composite Structures, 2003. 61: p. 247-253.
- Gdoutos, E.E., and I.M. Daniel Nonlinear Stress and Deformation Behaviour of Composite Sandwich Beams. Applied Mechanics and Materials, 2008. 13-14: p. 91-98.
- Kim, J., and S. Swanson, Design of Sandwich Structures for Concentrated Loading. Composite Structures, 2001. 52: p. 365-373.
- Frostig, Y., Baruch, M., Vilnay, O., and I. Sheinman, High-Order Theory for Sandwich-Beam Behavior with Transversely Flexible Core. Journal of Engineering Mechanics, 1992. 118.
- Frostig, Y., and M. Baruch, Bending of Sandwich Beams with Transversely Flexible Core. AIAA Journal, 1990. 28(3).
- Sokolinsky, V., and Y. Frostig, Nonlinear Behavior of Sandwich Panels with Transversely Flexible Core. AIAA Journal, 1999. 37(11).
- Swanson, S., and J. Kim, Comparison of a Higher Order Theory for Sandwich Beams with Finite Element and Elasticity Analyses. Journal of Sandwich Structures and Materials, 2000. 2: p. 33-49.
- Frostig, Y., and Y. Shenhar, High-Order Bending of Sandwich Beams with a Transversely Flexible Core and Unsymmetrical Laminated Composite Skins. Composites Engineering, 1995. 5(4): p. 405-414.
- Shenhar, Y., Frostig, Y., and E. Altus, Stresses and Failure Patterns in the Bending of Sandwich Beams with Transversely Flexible Cores and Laminated Composite Skins. Composite Structures, 1996. 35: p. 143-152.
- Sokolinsky, V., Shen, H., Vaikhanski, L., and S. Nutt, Experimental and Analytical Study of Nonlinear Bending Response of Sandwich Beams. Composite Structures, 2003. 60: p. 219-229.
- Swanson, S., An Examination of a Higher Order Theory for Sandwich Beams. Composite Structures, 1999. 44: p. 169-177.
- Yen, T.J., Fang, N., Zhang, X., Lu, G.Q., and C.Y. Wang, A micro methanol fuel cell operating at near room temperature. Applied Physics Letters, 2003. 83(19).
- Kakati, B.K., and V. Mohan, Development of Low-Cost Advanced Composite Bipolar Plate for Proton Exchange Membrane Fuel Cell. FUEL CELLS, 2007. 8(1): p. 45-51.
- Peairs, D., Hilton, C., Case, S., Lesko, J., Sitton, D., and R. Moffitt, Development of Prototype Pultruded Structural Fuel Cell. Composites Research Journal, Official Journal of the American Composites Manufacturers Association, Summer 2008. 2(3).
- Hilton, C., and J. Lesko, Optimization of Polar Plate/GDL Interfacial Contact Pressure for Improved Electrochemical Performance in Multiunctional Fuel Cells. Under final review by authors, 2009.
- Chang, W.R., Hwang, J.J., Weng, F.B., and S.H. Chan, Effect of clamping pressure on the performance of a PEM fuel cell. Journal of Power Sources, 2007. 166: p. 149-154.
- Zhang, L., Liu, Y., Song, H., Wang, S., Zhou, Y., and S. Hu, Estimation of contact resistance in proton exchange membrane fuel cells. Journal of Power Sources, 2006. 162: p. 1165-1171.
- Zhou, Y., Lin, G., Shih, A.J., and S.J. Hu, A micro-scale model for predicting contact resistance between bipolar plate and gas diffusion layer in PEM fuel cells. Journal of Power Sources, 2007. 163: p. 777-783.
- Ous, T., and C. Arcoumanis, Effect of Compressive Force on the Performance of a Proton Exchange Membrane Fuel Cell. Journal of Mechanical Engineering Science, 2007. 221(C): p. 1067-1074.
- J-H. Lin, W.-H.C., Y-J. Su, T-H. Ho, Effect of gas diffusion layer compression on the performance in a proton exchange membrane fuel cell. Fuel, 2008. 87: p. 2420-2424.
- https://bama.ua.edu/~rreddy/projects/fuel_cells.htm.
- Majumdar, A., and C.L. Tien, Fractal Network Model for Contact Conductance. Journal of Heat Transfer, 1991. 113: p. 516-525.
- Majumdar, A., and B. Bhushan, Fractal Model of Elastic-Plastic Contact Between Rough Surfaces. Journal of Tribology, 1991. 113(1).
- Mishra, V., Yang, F., and R. Pitchumani, Measurement and Prediction of Electrical Contact Resistance Between Gas Diffusion Layers and Bipolar Plate for Applications to PEM Fuel Cells. Journal of Fuel Cell Science and Technology, 2004. 1: p. 2-9.
- Ihonen, J., Mikkola, M., and G. Lindbergh, Flooding of Gas Diffusion Backing in PEFCs, Physical and Electrochemical Characterization. Journal of the Electrochemical Society, 2004. 151(8): p. A1152-A1161.
- Barbir, F., PEM Fuel Cells: Theory and Practice. Academic Press Sustainable World Series. 2005: Elsevier Academic Press. 433.
- Escribano, S., Blachot, J-F., Etheve, J., Morin, A., and R. Mosdale, Characterization of PEMFCs gas diffusion layers properties. Journal of Power Sources, 2006. 156: p. 8-13.
- Lee, S.-J., Hsu, C-D., and C-H. Huang, Analyses of the fuel cell stack assembly pressure. Journal of Power Sources, 2005. 145: p. 353-361.
- Wang, X., Song, Y., and B. Zhang, Experimental study on clamping pressure distribution in PEM fuel cells. Journal of Power Sources, 2008. 179: p. 305-309.
- Lai, C.-M., Lin, J-C., Hsueh, K-L., Hwang, C-P., Tsay, K-C., Tsai, L-D., and Peng, Y-M., On the electrochemical impedance spectroscopy of direct methanol fuel cell. International Journal of Hydrogen Energy, 2007. 32: p. 4381-4388.
- O’Hayre, R., Cha, S-W., Colella, W., and F. Prinz, Fuel Cell Fundamentals. 2006: John Wiley & Sons.
- Lee, W.-k., Ho, C-H., Zee, J.W. Van, and Murthy, M., The effects of compression and gas diffusion layers on the performance of a PEM fuel cell. Journal of Power Sources, 1999. 84: p. 45-51.
- Schwingshackl, C.W., Aglietti, G.S., and P.R. Cunningham, Experimental Determination of the Dynamic Behavior of a Multifunctional Power Structure. AIAA Journal, February 2007. 45(2): p. 491-496.
- Su, Z.Y., Liu, C.T., Chang, H.P., Li, C.H., Huang, K.J., and Sui, P.C., A numerical investigation of the effects of compression force on PEM fuel cell performance. Journal of Power Sources, 2008. 183: p. 182-192.
- Bazylak, A., Sinton, D., Liu, Z.-S., and N. Djilali, Effect of compression on liquid water transport and microstructure of PEMFC gas diffusion layers. Journal of Power Sources, 2006. 163: p. 784-792.
- Ge, J., Higier, A., and H. Liu, Effect of gas diffusion layer compression on PEM fuel cell performance. Journal of Power Sources, 2006. 159: p. 922-927.


