Damon R. Sparksa, David P. Beasona, Brandon S. Etheridgea, Jorge E. Alonsob, Alan W. Eberhardt a,*
aDepartment of Biomedical Engineering, University of Alabama at Birmingham, 1075 13th Street South, Hoehn 370, Birmingham, AL 35294-4440, USA
b Division of Orthopaedic Surgery, University of Alabama at Birmingham, 510 20th Street South, Faculty Office Tower 960, Birmingham, AL 35294-4440, USA
Abstract
Acetabular fractures are an especially problematic outcome of motor vehicle side impacts. While fracture type has been correlated with impact direction and femoral orientation, actual contact pressures in the hip joint have not been quantified for lateral loading conditions. In the present study, we used pressure sensitive film to measure contact areas and pressures in seven hip joints from four cadavers under quasi-static lateral loading through the greater trochanter. The aim was to quantify the interactions of the femoral head with the acetabulum associated with variations in femoral orientation. Three angles of hip flexion (80o, 90o, 100o) and hip abduction (o10o, 0o, 10o) were tested, producing nine test orientations for each joint. We observed that contact areas, pressures, and forces varied significantly with femoral orientation for the adducted hip. The principal locations of load transmission were in the anterior and posterior regions of the acetabulum. For the abducted femur, contact pressures were concentrated anteriorly, and with increased adduction, anterior contact pressures diminished while posterior and superior pressures increased. The movement of pressure sites was consistent with mechanisms of acetabular fractures described by Letournel and Judet and provides new data for validation of finite element models of the pelvis in side impact.
Keywords
Among vehicular collisions, automotive side impacts are the most common cause of pelvic fractures. During a side impact, occupants are struck laterally by intruding door structures, resulting in loading of the greater trochanter and the iliac wing. Lateral compression fractures [6,31] are the common result [14,21,28], involving various combinations of the pubic rami, sacrum, acetabulum, and iliac wings [10,11,14,15,21,27–29]. Among survivors, complicated intra-articular acetabular fractures are especially problematic, often requiring extensive hospital stays and immobilization [7]. Among these patients, secondary osteoarthritis is also common.
Introduction
Load path and femoral orientation have been related to patterns of acetabular fracture in clinical evaluations [18,30]. In a survey of motor vehicle collisions, Dakin et al. [11] observed a strong correlation between acetabular fracture type and impact direction. Letournel and Judet [18] described different types of acetabular fractures resulting from a blow to the greater trochanter as functions of femoral orientation. For example, increased abduction was linked with anterior wall and column fractures, while transverse, t-shaped fractures and fractures involving both columns resulted from trochanteric loading of the adducted femur. Actual spatial distributions and magnitudes of acetabular contact pressures during lateral loading, however, have not been quantified.
Pressure sensitive films have been used extensively to study hip contact in cadaveric specimens. Such studies have shown that contact during single legged stance is widely distributed across the acetabulum, with substantial pressure developed in the acetabular ‘‘roof’’ and the anterior and posterior regions of the acetabulum [1,3,22,33]. Congruence between the femoral head and acetabulum increases under larger loads, and pressure centers shift from the periphery to the inner lunate surface [1,33]. Finite element models have revealed that stresses during stance are transferred primarily through the dense bone along the anterior/superior ridge of the acetabulum, revealing a pelvic structure that is well suited for load transfer during ambulation [5,12]. Among existing finite element studies of side impact [4,13,20, 24,25], none considered the articular contact at the acetabulum. While these models were predictive of fractures of the pelvic ring, acetabular fractures were not addressed.
In the present study, we measured contact pressures and contact areas in human hip joints under quasi-static lateral loading through the greater trochanter with the femurs flexed in seated postures. The aim was to study the effects of femoral orientation on the resulting contact conditions. We hypothesized that femoral flexion and abduction angle would affect the resulting contact areas and pressures. We further conjectured that increased abduction of the femur would move contact anteriorly within the acetabulum, consistent with Letournel and Judet [18].
Materials and methods
Four fresh-frozen cadaveric pelves (three males—ages 62, 67, 68years; one female—age 73) were obtained through the Willed Body Program at the University of Alabama at Birmingham (UAB) with approval of the UAB Institutional Review Board. The pelves, which included L4 and L5 vertebrae and proximal femurs, were stored at -20oC and allowed to thaw to room temperature over 24h prior to testing. The pelves were cleaned of skin, muscle, and abdominal viscera, while leaving the pubic symphyses and sacroiliac joints intact. Throughout testing, specimens were kept moist by periodic application of saline solution. The hip joints were disarticulated by removing the iliofemoral, ischiofemoral, and pubofemoral ligaments [1], while leaving the labrum intact. The femoral ligament was resected to allow application of the pressure film to the femoral head. One joint with visible evidence of osteoarthritis was excluded, leaving seven healthy joints for testing
Low-grade Pressurex film (Sensor Products Inc., E. Hanover, NJ) with range 2.4–9.6MPa was selected for use based on preliminary tests on a trial pelvis that produced pressure stains for loads up to 1000N that contained the full range of stain intensity without visual evidence of excessive saturation of pigment. To minimize crinkle artifact, the film layers were cut into rosette patterns with dimensions based on the acetabular diameter [16,17,33]. A latex condom was first placed over the head of the femur, to which spray adhesive was applied to secure the pigment-containing film layer (the ‘‘C-layer’’) centered over the foveal notch. The stain-capturing layer (the ‘‘A-layer’’) was placed in contact with the C-layer, and a second latex layer was applied, which isolated the film from moisture.
The femur was secured in a
fixture comprised of an aluminum bar attached to a square pipe (Fig. 1). The linea aspera was aligned horizontally through the midline of the vertical walls of the square pipe, thus defining the neutral position in internal/external rotation. The femoral fixture was then attached to the actuator of an 858 Mini-Bionix Materials Testing System (MTS Systems, Eden Prairie, MN) with the longitudinal axis of the femur aligned parallel to the sagittal plane. The fixture allowed the flexion/extension angle of the hip joint to be varied. A threaded hole in the fixture allowed passage of a half-inch bolt, which was used to transfer load to the greater trochanter.
The vertebral column was potted in a cylindrical holder using PMMA and clamped into a custom-designed pelvis fixture (Fig. 1). The fixture consisted of a base track, a post, and a clamp that gripped the potted vertebral column and permitted the abduction/adduction angle of the hip joint to be manipulated through rotation of the pelvis about the vertebral axis. The base track functioned as an x–y table, allowing precise alignment of the acetabulum with the detached femoral head. Once in the fixture, each pelvis was placed at the desired abduction/adduction position and secured to the base plate. The pelvis was further supported at the contralateral ischium and along the contralateral iliac spine at the crest of the pubis to ensure that the positioning of the pelvis was consistent throughout the testing procedure.
Neutral abduction/adduction was defined with the longitudinal femoral axis perpendicular to an imaginary vertical line connecting the anterior superior iliac spines. Zero flexion was defined in the sagital plane, with the femoral axis oriented 20o from an imaginary tangent line extending from the S1 sacral vertebra. Pressure measurements were made at three flexion angles (80o, 90o, and 100o) and three abduction/ adduction angles (10o abduction, neutral, and 10o adduction).

Fig. 1. Pelvis positioned in the test fixture with the potted vertebrae clamped and contralateral side supported. The load was applied to the greater trochanter by a bolt attached to the femoral fixture, which was attached to the MTS actuator.
Pelvic and acetabular landmarks were recorded after a 10N compressive preload was applied. Marks were made on the film at the most inferior point on the femoral head and with reference to landmarks on the superior ramus and ischium, thus preserving the orientation of the film after it was removed. The joint was loaded to approximately 930N over a period of 60s. For optimum results (as specified by the film manufacturer), the applied load was held for 60s, during which time the rim of the acetabulum was traced onto the film. The load was then reduced back to 10N over an additional 60s. The femur was then carefully retracted from the acetabulum, and the pressure film was removed. The 930N load was based on preliminary tests, which revealed that 1000N was the maximum load accommodated by our test fixture, beyond which excessive pelvic deflection adversely affected the pressure measurements.
The stained films were stored in darkness for 48h after testing to avoid intensity fluctuations that can occur in the pigment [19], then digitized using an HP ScanJet 11cx/T digital scanner (Hewlett Packard, Palo Alto, CA) and Adobe Photoshop (Adobe Systems Inc., San Jose, CA). Once digitized, the images were saved as tiff files and loaded into Bioquant software (Bioquant Image Analysis Corporation, Nashville, TN), from which contact pressures were obtained for each stained pixel according to a second order calibration curve (Appendix A). The contact area distribution within the acetabulum was defined according to Letournel and Judet [18] by partitioning into anterior, posterior, and superior regions (Fig. 2). The average pressure was calculated for each region. Contact areas were measured using a tracing function in SigmaScan software (SPSS Science, Chicago, IL). Contact force was calculated by multiplying the measured contact area with the mean pressure for each stain.
Means and standard deviations of the contact area, mean pressure, and contact force were determined for each of the nine femoral test orientations. Multiple regression analyses were applied to study each factor as a function of femoral flexion/extension and abduction/adduction angles using StatView (SAS Institute Inc., Cary, NC). The level of statistical significance was designated as a = 0.05.
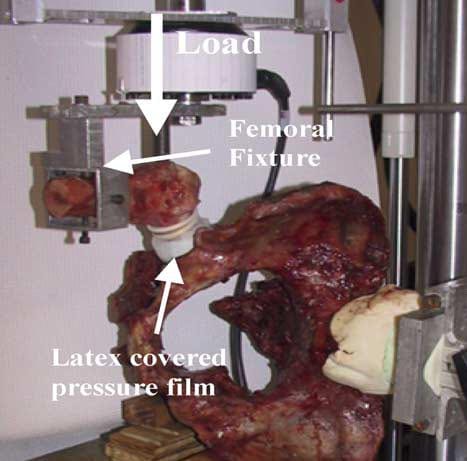
Fig. 2. Contact patterns were classified as anterior, posterior, or superior, according to their location within the acetabulum. Superior was defined as extending 60o posterior to the anterior-inferior iliac spine [12].
Results
Contact area
For the abducted femur, contact was concentrated anteriorly as evidenced by a dark dense stain (Fig. 3A). Increased adduction led to a reduction in the size and intensity of the anterior stain while the posterior stain darkened substantially (Fig. 3B). A superior stain became evident at 10o adduction (Fig. 3C) in most joints tested. The resulting pressure stains showed no signs of crinkle artifact.
Average contact areas for the entire acetabulum ranged from 1.76 to 2.61cm2 (Fig. 4). The smallest average total contact area occurred when the femur was oriented at 100o flexion and 10o adduction (100F/10Ad). The largest average total contact area occurred with the femur positioned in 80o flexion and 10o abduction (80F/10Ab).
An overall trend was observed in which contact area was largest in the posterior region of the acetabulum and smallest in the superior portion. Posterior contact occurred for all nine femoral positions. The mean contact area for this portion of the acetabulum ranged from 0.96cm2 at 90F/10Ab to 1.32cm2 for 80F/10Ad. No significant differences were found in posterior contact area for any femoral orientation (p = 0.3). In the anterior region of the acetabulum, the mean contact area reached a maximum value of 1.05cm2 at 80F/10Ab and a minimum of 0.56cm2 with the femur position at 90F/10Ad. Multiple regression revealed that increased adduction significantly reduced the contact area in the anterior region of the acetabulum (p < 0.02).
The mean contact area in the superior region of the acetabulum was smallest (0.04cm2) at 100F/10Ab and greatest (0.53cm2) at 80F/10Ad. When the femur was neutral or abducted, the superior region often did not participate in the transfer of load from the femoral head to the acetabulum. Superior contact area increased significantly with increased adduction (p < 0.007) and decreased significantly with increased flexion angle (p < 0.05)
Contact pressure
The mean pressure in the posterior portion of the acetabulum ranged from 2.22MPa at 90F/10Ab to 3.60MPa at 90F/0Ad (Fig. 5). At 10o adduction, the posterior pressures appeared to be greater than those found at the neutral and 10o abduction orientations, regardless of flexion angle, though the increase was not significant (p = 0.117).
The anterior acetabulum experienced a range of mean pressures from 3.03MPa at 80F/10Ad to 6.87MPa at 100F/10Ab. Multiple regression confirmed a significant increase in anterior pressure with increased abduction (p < 0.0001). The contact pressures remained relatively high at all flexion angles when the femur was oriented at 10o or neutral abduction. Changes in flexion angle did not significantly affect anterior pressures (p = 0.2542).< /p>
The pressure stains depicted a notable shift in load transfer from the anterior region of the acetabulum at 0o and 10o abduction to the posterior and superior regions at 10o adduction. Contact pressures in the superior region were substantially lower than those sustained by the posterior and anterior regions, except for the 80F/ 10Ad orientation. The mean pressure for this region ranged from 0.25MPa at 90F/0Ab to 2.16MPa with the femur oriented at 80F/10Ad. Regression analysis revealed significant increases in superior contact pressure with increased adduction (p < 0.008) and with decreased flexion (p < 0.04). Mean pressures less than the lower limit of 2.4MPa for the low-grade pressure film reflect the averaging process, where some load orientations did not produce stains and zero pressures were recorded.
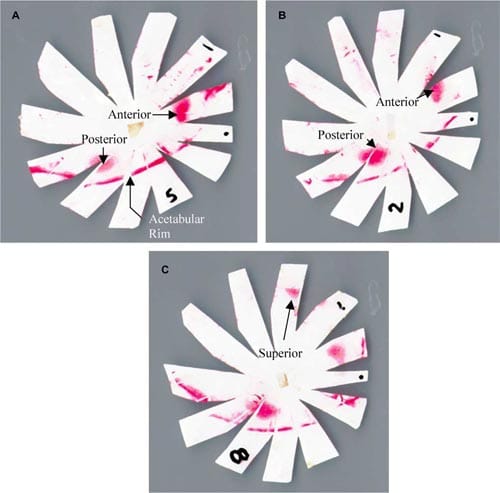
Fig. 3. Example pressure stains showing the transformation of contact patterns with increasing adduction: (A) at 90F/10Ab, the anterior stain was saturated, and a light posterior stain was visible; (B) at 90F/0Ad, the posterior stain density increased substantially while the anterior stain lightened; (C) at 90F/10Ad, the superior stain became evident, and the anterior stain density decreased substantially.
Contact pressure
The anterior portion of the acetabulum carried a larger portion of the applied load than the posterior region for 10o and 0o abduction (Fig. 6). At 10o adduction, however, the majority of the applied load was transferred to the posterior region. Mean posterior contact forces ranged from 242N at 90F/10Ab to 473N at 80F/10Ad, with significant increases (p < 0.03) for higher adduction angles. In the anterior region, the contact force ranged from 210N at 90F/10Ad to 550N at 90F/10Ab. This rise, which accompanied increased abduction, was significant (p < 0.0001).
The superior region of the acetabulum carried only a very small portion of the applied load, with values appreciably lower than those in the posterior and anterior regions. The average superior contact force ranged from roughly 8N at 100F/10Ab to 151N at 80F/10Ad. Multiple regression revealed significant increases in superior force with decreased flexion (p < 0.05) and increased adduction (p < 0.004).
Average total contact forces (mean pressure times area) ranged from 618N at 100F/10Ad to 1071N at 80F/0Ad. These values were 34% lower and 15% higher, respectively, than the average applied load of 930N. Typically the average calculated contact force was around 800N. When the femur was adducted 10o, the results most drastically underestimated the applied load and showed the greatest variance between test specimens.
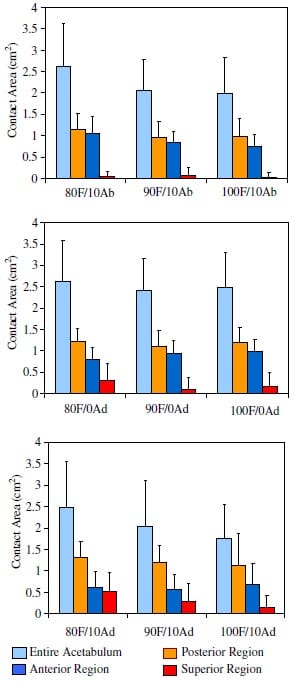
Fig. 4. Mean contact areas (bars represent std devs) for the different regions and the entire acetabulum.
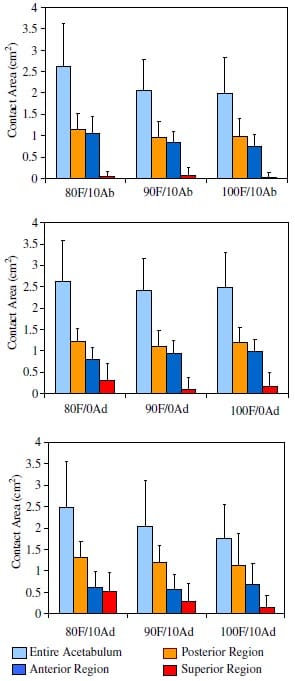
Fig. 5. Mean contact pressures (bars represent std devs) for the different regions and the entire acetabulum.
Discussion
The objective of the present study was to quantify the fundamental contact interactions of the femoral head and the acetabulum resulting from a lateral load applied to the greater trochanter, with the femur oriented at various angles of flexion and abduction. We observed that contact areas, pressures, and forces varied significantly with changes in hip abduction and to a lesser extent with flexion/extension angle, in support of our original hypothesis. Principal areas of load transmission in lateral loading were in the anterior and posterior regions of the acetabulum, with the superior region playing a relatively minor role in load bearing.
More specifically, this study showed that with the hip abducted 10o, the anterior region of the acetabulum carried a greater portion of the load than either the superior or posterior regions. The higher forces were a result of concentrated areas of high pressure. This finding is consistent with earlier portraits of load transmission through the ‘‘anterior horn’’ of the acetabular cartilage surface for the neutral or abducted femur [18]. While the posterior region displayed relatively large contact areas for the abducted femur, it transmitted substantially lower loads.
Notable changes in load transmission occurred as the joint was adducted past the neutral position. At 10o adduction, the posterior region of the acetabulum supported the majority of the applied load. An increase in the force transmitted through the superior region also occurred, as noted by Letournel and Judet [18], who described adduction as ‘‘increasingly affecting the roof of the acetabulum.’’ Variations in contact measures as a function of flexion angle were restricted to cases where the femur was adducted 10o. Otherwise, flexion did not significantly affect load transmission at the hip joint. We did not consider variations in internal/external rotation, however, which may also affect the resulting force transmission [18].
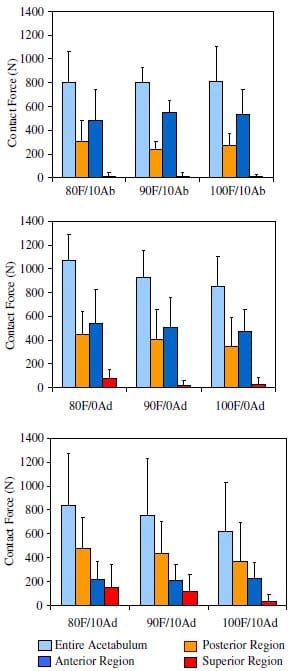
Fig. 6. Mean contact forces (bars represent std devs) for the different regions and the entire acetabulum.
Pressure film is an effective tool for quasi-static loading of the hip joint [1,3,16,17,22,33]. It was not designed, however, to capture the dynamic behavior of actual lateral impact events, with times to peak force less than 30ms in experiments [8,32] and in simulated falls [20,26]. Because articular cartilage is viscoelastic, the recorded pressures reflected the highest magnitude that occurred during the 60-s hold. Furthermore, the present quasi-static loadings would tend to overestimate dynamic (impact) contact areas and underestimate the corresponding contact pressures. Early analytical models of contact between biphasic cartilage layers [2,34] suggested that contact stresses do not change significantly during the first 200s of an applied step load. Later studies revealed, however, that the dynamic modulus of articular cartilage increased by up to a factor of two over the range of physiological loading frequencies [23]. This indicates that substantial decreases in contact area would be expected under impact loading rates, as compared to the present quasi-static conditions.
Experimental studies have shown that the average male pelvis will fracture at 10kN under lateral impact to the greater trochanter, while the 5th percentile female (50100, 106lb) pelvis will fracture at approximately 4kN [9]. These forces are 4–10 times greater than the 930N value used in our study. As stated previously, the test load was limited by our test fixture; higher applied loads rendered pressure measurements difficult and measurements were subject to shear artifact. With the 930N load applied, the pressure stains revealed peripheral contact areas, which indicates lack of congruity of the contacting surfaces. Higher forces would likely be accompanied by a centralization of the contact area, as demonstrated by others in experiments that simulated stance loading conditions [1,33]. Further testing at forces nearer to those experienced in real side impacts is certainly warranted.
In many measurements, the total contact force deviated substantially from the applied load of 930N. Sources of error include the averaging process, where contact forces were back calculated from mean pressures multiplied by total measured contact areas. Values exceeding 930N may be due in part to the angled orientation of
the contact surfaces and the fact that pressure film records the normal component of pressure. Some shear artifact might have occurred during the measurement process leading to erroneously high predictions. The potential for human error is reasonably high for pressure film techniques, which require repeated application of the multiple layers of latex and film. Contact forces less than 930N suggest the presence of extensive contact areas where the pressures were less than 2.4MPa and failed to register on the pressure film. These factors suggest a need for improved techniques for measurement of contact between the highly conforming surfaces of the human hip.
The present study was motivated by a paucity of biomechanical data relating contact stresses within the acetabulum to femoral orientation for seated occupants involved in automotive side impacts. While a number of finite element analyses of side impact have been performed [4,13,20,24,25], none of these attempted to model realistic hip contact; therefore, they could not predict the effects of varying hip flexion on acetabular contact and resulting fractures. It is our intent to employ the present experimental contact data to validate finite element models that may be used to investigate pelvic fractures in automotive side impacts.
Acknowledgments
The authors wish to thank Ken Mann, Gerald McGwin, Greg Dakin, Gerard Ateshian, Steven Olson, and Faris Bandak for their expertise and assistance in the execution of this study. Financial support was provided by the National Highway Traffic Safety Administration through the UAB Center for Injury Sciences.
Appendix A. Pressure film calibration
A calibration curve relating contact pressure to stain intensity was developed for the low-grade pressure film to account for our loading rate and the temperature and humidity in our lab [19]. Relatively uniform stains were achieved by using a special test apparatus that consisted of a 10.2cm2 aluminum plate, a 2.87cm diameter steel cylinder, a ceramic ball bearing, and the load cell mounted on the actuator of the MTS machine. The Cfilm (pigment-containing) was placed on the aluminum plate. The A-film was gently placed on top of this film, and the steel cylinder was carefully placed on top of the film layers. The ball bearing was placed between the load cell and the cylinder to reduce eccentric loading caused by misalignment. The MTS machine was utilized to ramp the load from zero to its maximum over 60s, hold the load at the maximum for 60s, and unload over 60s. Ten different loads were applied producing stains that spanned the pressure range of the low-grade film.
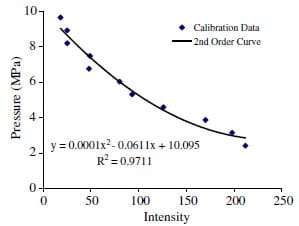
Fig. A.1. Second-order calibration curve for contact pressure versus stain intensity.
The stains were scanned and processed as described in the materials and methods. The image was transformed to grayscale, and a histogram of the image was produced. The mean pixel value was recorded along with the force that had been applied to that stain. The applied pressure, P, was calculated from P = F/A, where F was the applied load and A was the area of the steel cylinder. The pressure values were then plotted against intensity (Fig. A.1). The quadratic equation was fit to the data using a least-squares approach.
References
- Afoke NYP, Byers PD, Hutton WC. Contact pressures in the human hip joint. J Bone Joint Surg B 1987;69(4):536–41.
- Ateshian GA, Lai WM, Zhu WB, Mow VC. An asymptotic solution for the contact of two biphasic cartilage layers. J Biomech 1994;27(11):1347–60.
- Bay BK, Hamel AJ, Olson SA, Sharkey NA. Statically equivalent load and support conditions produce different hip joint contact pressures and periacetabular strains. J Biomech 1996;33(2):193–6.
- Besnault B, Guillermot H, Robin S, et al. A parametric finite element model of the human pelvis. In: Proc 42nd Stapp Car Crash Conf 1998. p. 33–46 [SAE 983147].
- Brown TD, Digioia AM. A contact-coupled finite element analysis of the natural adult hip. J Biomech 1984;17(6):437–48.
- Burgess AR, Eastridge BJ, Young JW, et al. Pelvic ring disruptions: effective classification system and treatment protocols. J Trauma 1990;30(7):848–56.
- Callaghan J. Biomechanics of the hip. In: Callaghan JJ, Dennis DA, Paprosky WG, Rosenberg AG, editors. Orthopaedic knowledge update: hip and knee reconstruction. Rosemont: American Academy of Orthopaedic Surgeons; 1995.
- Cavanaugh JM, Walilko TJ, Malhotra A, et al. Biomechanical response and injury tolerance of the pelvis in twelve sled side impacts. In: Proc 34th Stapp Car Crash Conf 1990. p. 1–12 [SAE 902305].
- Cesari D, Ramet M. Pelvic tolerance and protection criteria in side impact. In: Proc 26th Stapp Car Crash Conf 1982. p. 145–54 [SAE 821159].
- Conolly WB, Hedberg EA. Observations on fractures of the pelvis. J Trauma 1969;9(2):104–11.
- Dakin GJ, Eberhardt AW, Alonso JE, Mann KA. Acetabular fracture patterns: associations with motor vehicle crash information. J Trauma 1999;47(6):1063–71.
- Dalstra M, Huiskes R. Load transfer across the pelvic bone. J Biomech 1995;28:715–24.
- Dawson JM, Khmelniker BV, McAndrew MP. Analysis of the structural behavior of the pelvis during lateral impact using the finite element method. Acc Anal Prev 1999;31:109–19.
- Gokcen EC, Burgess AR, Siegel JH, et al. Pelvic fracture mechanism of injury in vehicular trauma patients. J Trauma 1994;36(6):789–95.
- Grattan E, Hobbs JA. Injuries to the hip joint in car occupants. Br Med J 1969;1(636):71–3.
- Konrath GA, Hamel AJ, Gueren J, et al. Biomechanical evaluation of impaction fractures of the femoral head. J Orthop Trauma 1999;13(6):407–13.
- Konrath GA, Hamel AJ, Sharkey NA, et al. Biomechanical evaluation of a low anterior wall fracture: correlation with the CT subchondral arc. J Orthop Trauma 1998;12(3):152–8.
- Letournel E, Judet R. Mechanics of acetabular fractures. In: Letournel E, Judet R, editors. Fractures of the acetabulum. 2nd ed. New York: Springer-Verlag; 1981.
- eLiggins AB. The practical application of Fuji prescale pressuresensitive film. In: Orr JF, Shelton JC, editors. Optical measurement methods in biomechanics. London: Chapman & Hall; 1997.
- Majumder S, Roychowdhury A, Pa S. Dynamic response of the pelvis under side impact load—a three dimensional finite element approach. Int J Crash 2004;9(1):89–103.
- McCoy GF, Johnstone RA, Kenwright J. Biomechanical aspects of pelvic and hip injuries in road accidents. J Orthop Res 1989;3(2):118–23.
- Olson SA, Bay BK, Hamel A. Biomechanics of the hip joint and the effects of fracture of the acetabulum. Clin Orthop 1997;393: 92–104.
- Parks S, Hung CT, Ateshian GA. Mechanical response of bovine articular cartilage under dynamic unconfined compression. Osteoarth Cartilage 2003;12:65–73.
- Plummer JW, Bidez MW, Alonso JE. Parametric finite element studies of the human pelvis: the influences of load magnitude and duration on pelvic tolerance during side impact. In: Proc 40th Stapp Car Crash Conf 1996. p. 17–28 [SAE 962411].
- Renaudin F, Guillemot H, Lavaste F, et al. A 3-D finite element model of pelvis in side impact. In: Proc 37th Stapp Car Crash Conf 1993. p. 249–59 [SAE 933130].
- Robinovitch SN, Hayes WC, McMahon TA. Prediction of femoral impact forces in falls on the hip. J Biomech Eng 1991;113:366–74.
- Schmidtke SZ, Bidez MS, Alonso JE. Acetabular fractures in automotive crashes: an initial report of 201 patients. Int Conf Pelvic Lower Extrem Inj 1995:81–94.
- Siegel JH, Mason-Gonzalez S, Dischinger PC, et
al. Safety belt restraints and compartment intrusions in frontal and lateral motor vehicle crashes: mechanics of injuries, complications, and acute car costs. J Trauma 1993;34(5):736–58. - States JD, States DJ. The pathology and pathogenesis of injuries caused by lateral impact accidents. In: Proc 12th Stapp Car Crash Conf 1968. p. 72–93 [SAE 680773].
- Tile M. Classification. In: Tile M, editor. Fractures of the pelvis and acetabulum. 2nd ed. Philadelphia: Williams & Wilkins; 1995.
- Tile M, Pennal GF. Pelvic disruption: principles of management. Clin Orthop 1980;151:56–64.
- Viano DC. Biomechanical responses and injuries in blunt lateral impact. In: Proc 33rd Stapp Car Crash Conf 1989. p. 113–41 [SAE 892432].
- Von Eisenhart-Rothe R, Eckstein F, Landgraf J, et al. Direct comparison of contact areas, contact stress and subchondral mineralization in human hip joint specimens. Anat Embryol (Berl) 1996;195(3):279–88.
- Wu JZ, Herzog W, Epstein M. Articular joint mechanics with biphasic layers under dynamic loading. J Biomech Eng 1998;120: 77–84.


