M. Borri-Brunetto, A. Carpinteri, and B. Chiaia
Department of Structural and Geotechnical Engineering,
Politecnico di Torino, Torino, Italy
Summary
The apparent shear strength of rock discontinuities is considerably smaller than that of small scale samples. At the same time, the sliding behavior is characterized, in situ, by marked instabilities, with the typical features of Critical Phenomena. Contact mechanics permits to calculate normal and tangential forces at any point, and to follow the stick-slip transition for arbitrary loading histories. On the other hand, the above aspects are not captured by the classical theories, including those based on roughness indices. We argue that the multiscale topology of contact domains plays a fundamental role in determining the behavior of rock joints. In particular, experiments and numerical simulations show that these domains are lacunar sets with fractal dimension smaller than 2.0. This provides peculiar scaling of normal and tangential pressures at the interface, and the consequent size-dependence of the apparent friction coefficient. Moreover, we implement Renormalization Group to determine the critical point (e.g. the critical shear force) when rock sliding occurs. We show that the critical force is less than the one predicted by the classical Coulomb’s theory, and that it depends on the specimen size and on the topology of the interface. The same reasoning can be extended to other phenomena, e.g., to the rupture of brittle materials.
Keywords: Slope stability, critical phenomena, scale effects.
1. Introduction
October 9, 1963, 10.39 pm – TheVajontDamin the northern Italian Alps. 275 millionm3 of rock slid into the 115 million m3 of water in the reservoir, which was about two thirds full. The sliding mass travelled as a sheet of undisturbed rock formations at maximum speed that has been variously estimated between 90 and 250 km=h. A water wave was created which overtopped the dam by 70 m, obliterating several villages and killing 1925 people in the River Piave valley. Between the end of construction (1960) and the tragic event (1963) rock creep (i.e. partial slips) had been observed, in the direction of the slope, in the dolomitic limestones on the southern flank of the valley. Initially, the rate of creep was 1 cm=week, but gradually it accelerated to 1 cm=day and finally to about 80 cm=day. In the following years similar high-velocity rock slides occurred in the Italian Alps (e.g. rockslides in Valtellina, 1987), characterized by apparent unpredictability and a huge loss of human lives.
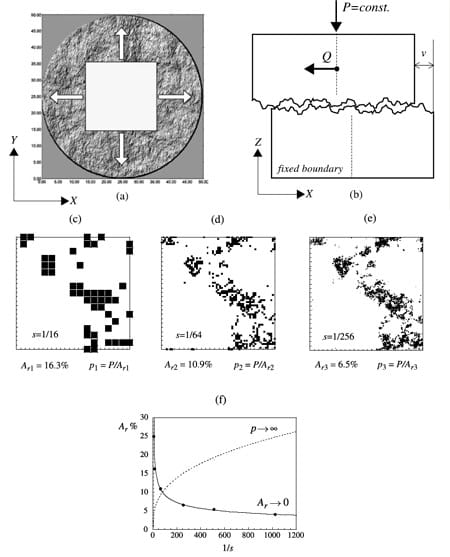
Fig. 1. Multiscale analysis of contact mechanics at a rock interface (a, b). Lacunarity of the contact domain: detail of three numerical results obtained at different resolutions (c, d, e). The calculated fractal dimension, in this case, is Δs=1.39. Power-law dependence of the real contact area Ar% and of the corresponding real mean pressure p (at the same external load) on the resolution (f), see also Eq. (1)
Two aspects can be evidenced in these phenomena. First, the dynamics of sliding activation follows a typical critical behavior, e.g. partial slips occurred, with progressively larger extent, before the final catastrophic sliding. Secondarily, when the shear strength of small rock samples was measured in the laboratory, it appeared significantly higher than the strength activated in the rockslides, e.g. sliding should not have occurred according to the measured values.
The study of the atomic origins of friction, or nanotribology, has been long neglected by physicists, and only in the last few years gained adequate interest (Krim, 1996). At the opposite level, the macro-scale, engineers have usually been content with the classical laws of Coulomb and Amontons. According to their hypotheses, the frictional force is proportional to the normal load and, less intuitively, it does not depend on the apparent area of contact An. Indeed, it has long been known that the shear strength of rock discontinuities depends on roughness. Among the various criteria to estimate the influence of roughness, an empirical quantity named joint roughness coefficient (JRC) is the most used in practice (Barton, 1973). However, a remarkable size-scale effect on the JRC (and thus on the shear strength) has been early reported. Satisfactorily explanations for this size-effect have not been found up to now (Pinto da Cunha, 1993). Within the classical hypotheses, in fact, the frictional force Q between two rough surfaces is independent of the nominal contact area A0, but depends on the true contact area (Greenwood and Williamson, 1966), which, in turn, is proportional to the normal load P (Q¼fP, where f is the friction coefficient). Thus, if we consider two joints of different sizes, under the same nominal pressure Po=P/An, the same value of the critical shear force is predicted.
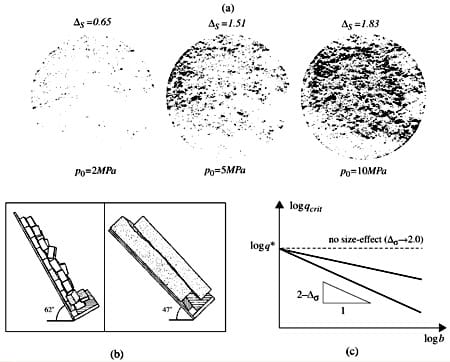
Fig. 2. a Experimental contact domains obtained in a natural rock joint by means of a pressure-sensitive film at a mean apparent stress of respectively 2, 5, and 10MPa. The fractal dimensions have been calculated according to the box-counting method. b Scheme of a tilt test on rock discontinuities, yielding the decrease of the apparent friction coefficient. c Fractal interpretation of the experimentally observed decay of the limit shear stress with increasing normal load
When two rough bodies are pushed into contact, a set of contact points, with a complex pressure distribution, is generated. If the interacting surfaces are self-affine, which is the case for fracture surfaces in natural rocks (Mandelbrot, 1985), the contact domain is a self-similar lacunar set (i.e., a point set characterized by a fractal dimension less than 2.0). In other words, in the presence of multiscale elastic asperities, the contact domain is not a compact euclidean area, which is the hypothesis at the basis of the classical theories, but it rarefies as the resolution increases (Fig. 1c, d, e). Lacunarity of the contact domain has been proven by experimental tests, e.g. by means of metal infiltration techniques (Cook, 1992). We used, instead, a pressure-sensitive film (Pressurex® by Sensor Products Inc.) on small samples of fine-grained sandstone (Fig. 2b). We believe that the infiltration technique presents a drawback because some areas where contact does not occur might be completely surrounded by contact ‘rings’, which prevent the flow of the liquid metal.
2. Lacunar Contact Domains
We have developed a multiscale algorithm to determine the set of points where contact occurs (i.e. the contact domain) and the pressure at any point of a rough interface (Bo
rri Brunetto et al., 2001). When the evolutive contact problem is solved for a given interface at different values of discretization r, the resulting contact domains Sr can be compared (Fig. 1). It is clear that the concept of area of true contact (Greenwood and Williamson, 1966) is not able to describe in a scale-independent manner the contact interactions, since it tends to zero in the limit of r!0. Therefore, we abandon the euclidean description and move to the fractal model, characterized by a noninteger dimension ΔS≤2.0 of the domain S. Accordingly, let us consider the following group equation:
where P is the applied normal load, Ar and pr are respectively the real contact area ([L]2) and the real mean pressure ([F][L](2) measured at the resolution r, A0 is the apparent (nominally flat) area and p0=PA is the apparent mean pressure at the macro-scale. As one can realize from Fig. 1, whatever the value of the normal load P, pr increases with increasing resolution and tends to infinity as r→ 0, because the euclidean measure ([L]2) of the contact domain S vanishes. Hence, in the limit of the highest resolution, the classical definition of area loses its significance. It is instead advantageous (Carpinteri, 1994) to introduce the fractal measure As* of the domain S, univocally defined by the noninteger dimension [f][L]-Δs . Correspondingly, the fractal mean pressure p* can be defined, for each value of P, as the anomalous pressure acting at the fractal interface with noninteger dimensions [F] [L]-s . From Eq. (1), if b is a characteristic linear size of the interface, the following scaling law is provided:
The fractal mean pressure p* represents the true scale-independent quantity in the description of normal contact of rough surfaces. Two interfaces exchanging the same value of p* are assumed to behave similarly. When a tangential force Q is applied, tangential stresses q develop at contact points. At the limit state, the apparent shear strength qcrit=Qcrit=fpo is activated. Therefore, qcrit must scale according to:
where q* represents the fractal limit shear stress. Two specimens of different sizes, extracted from the same rock joint, will slide when the value q* is attained. Thus, according to Coulomb’s law, the apparent friction coefficient f for the smaller specimens will be larger than the value measured on the larger sample. According to Eq. (3), the above size-effect tends to disappear as the domains become more dense (i.e., as ΔS tends to 2.0), which may occur by reducing the roughness or by increasing P (see Fig. 2).
3. Criticality and Renormalization Group
Another issue is represented by the criticality associated to the sliding phenomenon (Persson and Tosatti, 1996; Bak et al., 1988; Rice and Ruina 1983). A simple Renormalization Group (RG) calculation, based on scale invariance (Wilson, 1971), permits the critical value of the shear force which provokes the instability to be found. Criticality already appears in other approaches (Wang and Scholz, 1993; Johnson, 1997), where the multiscale mechanisms were not considered. Our approach, although similar to the one proposed by Smalley et al. (1985), differs for two reasons. First, we deal with a (lacunar) fractal domain of contact points instead of an euclidean array of asperities (e.g. self-similarity is not an assumption, but is inherent to the model). Moreover, if Coulomb friction is supposed to hold at the asperity level, we do not need to make assumptions on the strength distribution, since we exactly know, at any point, the value of the normal force and thus of the limit shear stress. This implies that we are dealing with meso-scale asperities (e.g. r>1 mm), which is a realistic range for natural rock surfaces. In the presence of micro- or nano-asperities (e.g. r <1 mm), the same RG method could be applied by assuming a local adhesion mechanism instead of friction.
After calculating the tangential stresses q at any point of the contact domain, for a given value of the external tangential force Q, we determine the point with the highest q=qlim ratio. The external load is re-scaled to make this point reach exactly its critical condition. Once the first point has slipped, a certain amount of the tangential stress it was carrying needs to be redistributed. The multi-scale transfer of stress from a point which has slipped to the nearest asperities is the essential feature of the model (see the RG methodology described below). From the physical point of view, stress transfer may be ascribed to the elastic energy release due to micro-slip or to the drop of the friction coefficient. Without stress transfer, the behavior of the system is trivial and coincides with the classical theory. We adopted a redistribution coefficient β controlled by the drop of the friction coefficient (see Fig. 3e).
For a given applied shear force Q, the correlation length ξ can be considered as the maximum linear size of the cluster of slipped points. Two situations may occur (Fig. 3). Micro-slip events can be confined below a certain scale (partial-slip), or can spread virtually to any scale (full-sliding). In the former case, the correlation length ξ is finite and can be computed. The separating value of the shear force is the critical shear force Qcrit, which can be calculated numerically. When Q¼Qcrit, the correlation length diverges according to a power-law and full-slip occurs. The critical value is reached much before all the points have attained their critical condition. Therefore, contrarily to the classical theory, the limit shear value is smaller than the sum of the local shear strengths or, which is the same, the apparent global friction coefficient (fglob=Qcrit=P) is smaller than the microscopic one f.
The fractal hierarchical model is built up according to the scheme reported in Fig. 3, and can be obtained by overlapping subsequent box-coverings of the contact domain. The first-order cell (micro-scale) corresponds to the finest resolution (which is 1=256 in the picture, although the finest simulations were equal to 1=1024), and subsequent orders are obtained by dyadic sequence. At the rth scale of observation, a generic contact point corresponds to several contact points at the lower scale (r-1)th. Some cells are blank (i.e. there is no asperity) due to the lacunarity of the contact domain. Once a point has slipped, the friction coefficient drops to a value f1 βf, where β <1 is the redistribution coefficient and qres is a residual strength. An amount of stress equal to (1-β)fp has to be redistributed among the contact points in the cell. As a first approximation, we assume that this quantity is equally carried by the rest of the contact points in the cell. If another point, in the same cell, reaches its critical condition, it slips too, and some extra shear stress must be transferred.
According to renormalization, we assume that an rth order cell slips only if all the corresponding points at the (r-1)th level have slipped. This circumstance depends on the applied shear stress, but also on the spatial distribution of the contact points and on the distribution of normal micro-forces. The same calculations are repeated at subsequently larger scales, the collective behavior at a certain level representing the input for the larger one. Nonlinear regression of the numerical data yields a family of Sshaped curves like the one depicted in Fig. 3. The straight line corresponds to: Nslip(r)/Ntot(r)=Nslip(r=1
)=Ntot(r+1). The points 0 and 1 are the stable fixed points of the system, corresponding respectively to full-stick and full-sliding. The iterative relation crosses the straight line at point C, which is an unstable fixed point, i.e. the critical point separating the basin of (stable) partial-slip from the basin of (unstable) full-sliding.
The critical value (Nslip=Ntot)crit depends on the external load, on the density of the contact domain, and on the friction mechanisms activated by the asperities. A direct relation exists between (Nslip=Ntot)crit and the ratio Qcrit=Qnom. It is interesting to compare the value of the critical shear force Qcrit with the value of the nominal strength of the interface Qnom as predicted by the classical theory, which is equal to the sum of the local shear strengths, i.e., to Qnom=fP. For the contact domain depicted in Fig. 3a, in the case of β=0.8 we have obtained Qcrit=0.89Qnom. In the case of β=0.7, Qcrit is equal to 0.76Qnom, and for β=0.6, Qcrit is only 0.49Qnom. Thus, as one could easily expect, the higher the stress redistribution, the smaller the critical load.
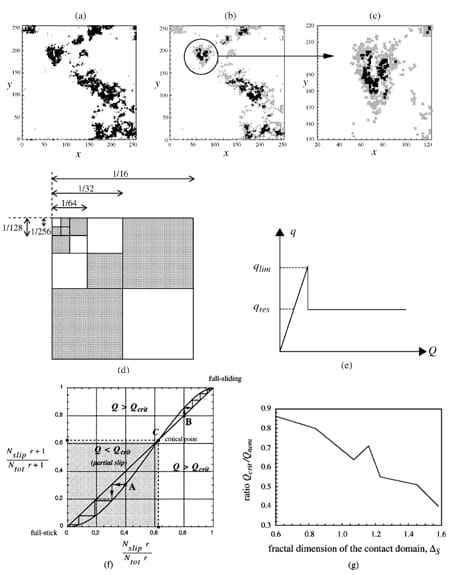
Fig. 3. Elastic theory of tangential contact: extent of the stick (black) and slip (grey) areas of contact for two increasing values of the applied shear force Q (a, b). Enlargement of a zone in the second contact domain (c). According to the classical theory, the slip area propagates from the external parts towards the inner parts of the contact domain. Scheme of the renormalization procedure (d), and of the drop of friction coefficient for slipped points (e). Graphical interpretation of the RG methodology (f). Point C corresponds to the value 0.62. If the ratio Nslip=Ntot is smaller than the critical value (e.g., if Nslip(r)=Ntot(r)¼0.4, point A), the solution iterates to Nslip¼0 at larger scales. This means that slipping is confined to micro-scales and macroscopic sliding does not occur. Instead, if Nslip=Ntot is larger than the critical value (e.g., if Nslip(r)=Ntot(r)¼0.8, point B), the solution iterates to Nslip=Ntot¼1, i.e. microscopic slip events yield full-sliding at the macroscopic scale. Calculated decrease of the ratio Qcrit=Qnom as the fractal dimension of the contact domain increases (g)
Numerical calculations on contact domains with different dimensions ΔS, show that the larger ΔS (i.e., the smaller the composite roughness of the interface), the larger the value of Qcrit. This is in agreement with the results by Chow (2001), who reported that the limit adhesion, at nano-scales, increases by orders of magnitude if the interfaces are made smoother. On the other hand, the larger ΔS, the smaller the ratio Qcrit=Qnom (see Fig. 3g). This means that, in the case of rarefied contact domains, the partial-slip stage can develop more efficiently than in the case of dense euclidean domains, and thus the transition to full-sliding is more ductile. This can be explained by the presence of large zones (lacunae) where contact does not occur and stress transfer to larger scales is hindered. These zones play the role of ‘slip-arresters’ (this resembles the crack-arresting mechanisms of some fibrous materials, where energy release is not transmitted integrally by broken fibres to the adjacent ones (Harlow and Phoenix, 1982).

Fig. 4. Experimentally detected size-scale effects on the friction coefficient (after Bandis et al., 1981). Notice the higher peak shear stress and the steeper post-peak branches for the smaller specimens (a). Powerlaw fitting of experimental data (b, c). According to Eq. (3), the fractal dimension of the contact domain at incipient sliding is equal to ΔS=1.77 for the first data set and to ΔS=1.61 for the second data set. The theory correctly predicts that, the smaller the fractal dimension of the contact domain, the more pronounced the size-scale effect on shear strength
In order to validate the theory, the experimental shear tests on rock joints made by Bandis et al. (1981) are shown in Fig. 4. Not only do larger specimens show lower shear strength under the same normal load, but also do the post-peak curves become progressively steeper (i.e. more unstable) as the nominal contact area increases. Both phenomena can be explained by means of the multiscale model, according to the sizeeffect on the nominal friction coefficient f and to the higher lacunarity of larger samples, which provides a ‘‘more ductile’’ transition to full-sliding. Power-law fitting of the experimental data eventually permits the fractal dimension ΔS of the contact domain to be found (Fig. 4b, c).
4. Conclusions
The occurrence of criticality in the (static) frictional behaviour of rough rock interfaces has been verified by a numerical Renormalization Group approach. In particular, stress transfer due to partial slip of asperities has been taken into account. In this way, the onset of full-sliding is characterized by a marked instability, with all the features of a critical transition. The main role played by disorder in the phenomenon has been put into evidence. In particular, the contact domain is a fractal lacunar set, with measure and dimension depending on the composite roughness of the contacting surfaces and on the normal load. The onset of sliding depends not only on the fractal measure A*(S) of the contact domain, but also on the stress transfer mechanism adopted and on the box-dimension of the domain. The maximum sustainable shear force, at a fixed value of the normal load, increases with increasing the measure of the domain. Less intuitively, the ratio Qcrit=Qnom decreases with increasing the fractal dimension ΔS of the contact domain, i.e. lacunarity delays the sliding instability.
Moreover, a fractal (scale-independent) Coulomb’s law has been put forward, which implies that the nominal friction coefficient undergoes size-effects, i.e., it decreases with increasing the size of the contacting surfaces. Real rock slopes (e.g., in the range between 10 and 1000 m) are in fact characterized by a nominal friction coefficient considerably smaller than the one measured on laboratory specimens (e.g., in the range between 10 and 100 cm). Experiments show that transition to full-sliding in large samples is less abrupt than in smaller specimens, as is adequately modelled by the proposed theory.
References
- Bak, P., Tang, C., Wiesenfeld, K. (1988): Self-organized criticality. Phys. Rev. A 38, 364–374.
- Bandis, S., Lumsden, A. C., Barton, N. R. (1981): Experimental studies of scale effects on the shear behavior of rock joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 18, 1–21.
- Barton, N. (1973): Review of a new shear strength criterion for rock joints. Eng. Geol. 7, 287–332.
- Borri-Brunetto, M., Chiaia, B., Ciavarella, M. (2001): Incipient sliding of rough surfaces in contact: a multiscale numerical analysis. Comput. Meth. Appl. Mech. Engng. 190, 6053–6073.
- Carpinteri, A. (1994): Fractal nature of material microstructure and size effects on apparent mechanical properties. Mechanics Mater. 18, 89–101.
- Chow, T. S. (2001): Nanoadhesion between rough surfaces. Physical Rev. Lett. 86, 4592–4595.
- Cook, N. G. W. (1992): Natural joints in rock: mechanical, hydraulic and seismic behavior and properties under normal stress. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 29, 198–223.
- Greenwood, J. A., Williamson, J. B. P. (1966): The contact of nominally flat surfaces. In:
Proc., Royal Society London A 295, 300–319. - Harlow, D. G., Phoenix, S. L. (1982): Probability distributions for the strength of fibrous materials under local load sharing. Two-level failure and edge effects. Adv. Appl. Probab. 14, 68–94.
- Johnson, K. L. (1997): Adhesion and friction between a smooth elastic spherical asperity and a plane surface. In: Proc., Roy. Soc. London A 453, 163–179.
- Krim, J. (1996): Friction at the atomic scale. Scientific American 65, 48–56.
- Mandelbrot, B. B. (1985): Self-affine fractals and fractal dimension. Physica Scripta 32, 257–260.
- Persson, B. N. J., Tosatti, E. (eds.) (1996): Physics of sliding friction. Kluwer, Dordrecht.
- Pinto da Cunha, A. (ed.) (1993): Scale effects in rock masses. Balkema, Rotterdam.
- Rice, J. R., Ruina, A. L. (1983): Stability of steady frictional slipping. J. Appl. Mech. 50, 343–349.
- Smalley, R. F., Turcotte, D. L., Solla, S. A. (1985): A renormalization group approach to the stickslip behavior of faults. J. Geophys. Res. 90, 1894–1900.
- Wang,W., Scholz, C. H. (1993): Scaling of constitutive parameters of friction for fractal surfaces. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 7, 1359–1365.
- Wilson, K. G. (1971): Renormalization group and critical phenomena. Physical Rev. B4, 3174–3205.


