P. Heger, R. Bossert, J. Carson, S. Delchamps, K. Ewald, H. Fulton, J. Kerby, W. Koska, J. Strait and M. Wake
Fermi National Accelerator Laboratory
Abstract
Collet end clamps employed on full length and model SSC dipole magnets designed and built at Fermilab are described. Experimental data are presented for the baseline Fermilab design. Tests using pressure sensitive film to register the midplane and pole coil pre-stresses in the end clamp region are reviewed. Theoretical calculations address end clamp mechanics at room temperature, liquid helium temperature, and under magnetic excitation.
Introduction
Fermilab 50mm aperture SSC Collider Dipole Magnets have three splices at the lead end. Collet end clamps [l,lOl are used to achieve continuous support of coils and splices in the end region; they prevent coil motion which could result in a quench. This region is subjected to gradients in prestress, magnetic field and Lorentx. forces. In the Fermilab SSC 40 mm aperture model dipole program, magnet performance was sometimes limited by quenches occurring in the end clamps, in particular near the inner to outer coil splices [21. In contrast, very few quenches have been observed in the end clamps designed for the 50 mm aperture model and full length magnets built to date at Fermilab [3,4,51.
The purpose of this paper is to better understand the performance of the end clamps by comparing models of the end clamp mechanics to experimental data. During construction of full length and model magnets, the change in external diameter of the end clamps upon installation is measured, giving an indirect indication of coil stresses in the end clamp. In separate tests, pressure-sensitive tape was used to measure pole and midplane stresses in the end clamp directly, and an attempt was made to correlate the observed stresses with changes in end clamp diameter. In this paper, these measurements are compared with mechanical models which predict end clamp deflection as a function of coil prestress. The analysis was taken one step further by using the models to predict changes in coil stress under cooldown and magnetic excitation.
End Clamp Design
The Fermilab 50mm dipole end clamp design [l], at the magnet’s lead end, is shown in Figure 1. The coil straight section extends 76 mm into the end clamp. The coils then make the turn from quadrant to quadrant. Inner to outer coil splices are held by cutouts in the four G-10 collet quadrants which surround the coils; the upper to lower outer coil splice is held by a G- 10 splice housing and cover. The collet quadrants are separated azimuthally by approximately 0.81 mm
The outer surface of each collet has a 2 degree taper; the end can has the same taper on its inner surface. This taper allows the end can to be slid over the collet quadrants from the collared coil assembly side. The end can directs a radial force onto the collet quadrants which radially clamp the coils and a set of G-10 “key” pieces. This induces a compressive azimuthal load, generally referred to as “prestress.” The splice housing, cover, and end cap are then positioned and the latter is welded on the end can. A similar design is used at the return end, where there are no splices.
The prestress induced during assembly is reduced during cooldown from 300K to 4K. Lorentz forces during magnetic excitation lead to further changes in coil stress. The magnitude of the Lorentz force is proportional to current and to the dominant dipole field. The current is the same in the end region as it is in the straight section. The dipole field, however, is 6.6 T in the collared portion of the magnet and falls off to 4.8 T at a distance of 38.1 mm into the end clamp [6]. Lorentz forces in the following model are scaled down to 4.8/6.6 or 73% of those in the collared coil section. (All models in this paper examine end clamp mechanics at a distance of 38.1 mm into the end clamp. This location is far enough from the end of the collared section to eliminate influence from the collars, but it still lies within the coil straight section.)
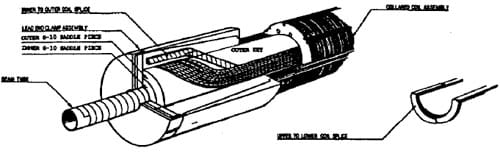
Figure 1a. End Clamp Assembly – Lead End
Experimental Data
Measurements On Model and Full Length SSC Dipoles
The clamping applied to the coils during assembly was monitored by measuring the change in outer diameter of the end can before and after assembly onto the coils. The change or “deflection” in diameter of the end cans was measured on a total of twenty-six end clamps (nine full length and four model magnets). End can diameter deflections were taken at azimuthal locations of 0, 45, 90, and 135 degrees at a distance of 38.1 mm from the collared section. An average diameter was also measured using a pi-tape.1
section. An average diameter was also measured using a pi-tape.1 The results of the end can diameter deflection measurements are shown in Figure 2. More detailed data for the full length magnets is given elsewhere 171. The average lead end vertical, horizontal, and pi-tape deflections are 0.10, 0.04, 0.10 mm respectively. The corresponding return end values are 0.13, 0.04, and 0.08 mm. (The uncertainty of each individual deflection measurement is about M.02 mm.)
The standard deviations of lead and return end vertical, horizontal, and pi-tape deflections for the entire set of lead and return end clamps are 0.05, 0.04, and 0.04 mm respectively. In an attempt to compensate for variations in collet quadrant inner diameter, various amounts of radial kapton shim, ranging from 0 to 0.25 mm, were placed between the collet quadrants and the outer coil surfaces. Some of the large variation in end clamp deflection may arise from the uncertainty in this procedure.
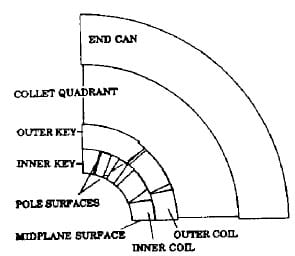
Figure 1b . End Clamp Cross-Section
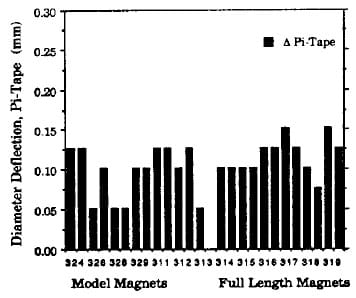
Figure 2. Diameter Deflection Measurements
Test Installations with Pressure-Sensitive Film
The most direct measure of coil prestress inside the end clamps was made using pressure-sensitive film. It was applied to the outer coil at the key/coil interface (pole) and to the inner and outer coils at the upper/lower coil interface (midplane). Contact pressure and diameter deflection were measured as the end clamp was installed eight times on the coils of model magnet DSA322. With each installation, new pressure sensitive film was applied. The presence of the film did not create additional prestress because its thickness was dimensional
ly compensated by removing 0.13 mm (5 mils) of azimuthal kapton. No film was applied to the inner coil pole because this dimensional compensation was not possible at this location.
Figure 3a. Average Fuji Film Pressure
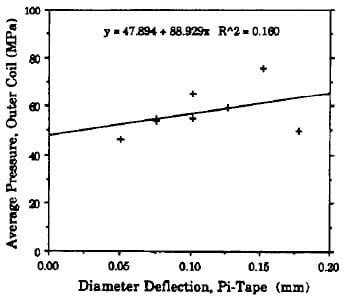
Figure 3b. Average Fuji Film Pressure versus Diameter Deflection Measurements
The pressure-sensitive film used was Fuji Prescale HS-H 181. It consists of a polyester backing coated with an emulsion containing colorant capsules which burst under pressure, releasing a chemical which turns red when it mixes with a developer also .contained in the emulsion. The final color of the film corresponds to the highest pressure to which the film has been exposed. The film is scanned with a device which converts the color intensity to a contact pressure. The manufacturer’s calibration of the scanning device (Fuji Prescale Densitometer, FPD301) was checked at Fermilab by taking readings on tape exposed to known pressures. All end clamp coil pressure readings were adjusted to follow this second calibration.
The measured pressures, averaged over the outer coil midplane and pole surfaces, are plotted individually and against the pi-tape deflection for ‘all eight installations (Figures 3a and 3b). [9] The uncertainty in the pressure readings is estimated to be ± 7 MPa (±1OOOpsi). The average outer coil pole and midplane stresses are 64.1 MPa (9300 psi) and 63.8 MPa (9250 psi) respectively. A linear curve fit shows a 11.8 MPA (1700 psi) increase in prestress for every 0.13 mm increase in end can diameter deflection. Nearly equal average pole and midplane stresses are consistent with the simple model of an azimuthal spring in a frictionless cavity.
Exposed films show that there are stress gradients of two kinds; large gradients due to variation in cable insulation thickness and gradients from the inner to outer edges of the midplane surfaces. The stress gradient across the midplane surfaces is greater than that across the pole face; this is predictable because the angle at the pole is less than radial and therefore the coil has to bend less to conform a circular shape.
Quench Behavior
During cooldown and cold testing, no coil stress measurements or end can defections could be made; nonetheless, quench behavior is the most crucial measure of end clamp performance. There were only two quenches in the end clamp regions of full length 50mm magnets. They occurred in magnets DCA313 and DCA314. No end clamp quenches occurred in 5Omm model magnets except during high ramp rate studies[4,5].
Mechanical Models
Spring Models
Interpretation of the magnet measurements is aided by simple mechanical models. On a small scale, the coil/key structures can be represented as an azimuthal spring. The coils have a smaller elastic modulus and larger length than the G-10 keys (see Table 1); therefore, they are weaker springs which will compress more under azimuthal force.
Thin-Walled/Thick-Walled Cylinder Models
The mechanics of the entire assembly may be simplified by representing the inner coil, outer coil, and end can as thin-walled cylinders. For a given outer coil stress, there is a corresponding external pressure. This pressure is scaled by the ratio of diameters and applied as an internal pressure on the end can. For this internal pressure there is a corresponding diameter deflection. (Calculations are simplified here by substituting the modulus of the coils for that of the G-10 keys as well.) A more precise relation between prestress and end clamp diameter deflection is derived by considering the variation in azimuthal and radial stress through the width of the coil. This effect is accounted for in equations which describe thickwalled cylinders. Differences between thin- and thick-walled cylinder predictions are shown in Figure 4. It should be noted that a diameter deflection predicted in such a manner is an average value. As described above, the end can actually distorts to an oval shape. However, this rough estimate provides good correlation with measured pi-tape deflections.
Finite Element Model
Finally, a 2-D finite element model (Figure 5) further refines the azimuthal stress contour by including the effect of the non-radial angle at the pole and the prestress loss due to the flexibility of the end can. The relation between outer coil prestress and end can deflection is also given in Figure 4.
The end clamp is symmetric about horizontal and vertical planes, thus one quarter of its cross-section is modeled. Symmetry conditions are imposed on the end can at the horizontal and vertical plane and also on the G-10 keys at the vertical plane. Azimuthally oriented gap elements transfer force from the coils to the key. Radially oriented gap elements transfer azimuthal pressure from the inner coil and key to the outer coil and key, from the outer coil and key to the collet quadrant, and from the collet quadrant to the end can. The geometry corresponds to the cross-section at a distance of 38.1 mm from the end of the collared coils.
The assembly process is represented by displacing the coils azimuthally at their midplane until the desired average prestress is achieved.2 The prestress input to the outer coil is 64 MPa (9300 psi), corresponding to the average of the outer coil pole and midplane prestress measured with Fuji film on model magnet DSA322.
To demonstrate the validity of inducing prestress through midplane displacements, two test cases were run: one with coils displaced AR radially and one with coils displaced ΔRπ/2 at the midplane. Resulting prestress values are within 4% of each other, which is within the precision of the Fuji tape itself. In both cases the ratio of inner to outer coil stress is approximately 1.6:1; this ratio is reduced to 1.5:1 when the end can and collets are added to the model.
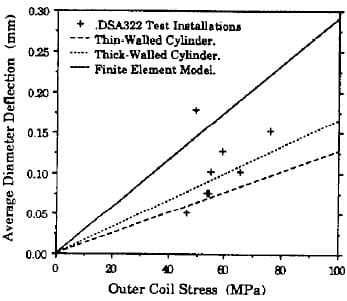
Figure 4. Diameter Deflection versus Prestress
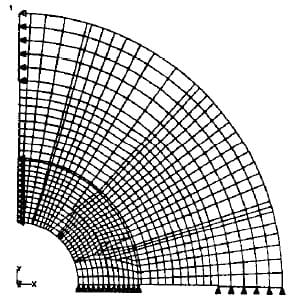
Figure 5. 2-D Finite Element Model

Table 1. End Clamp Components – Material Properties
Prestress Loss During Cooldown. The collet quadrants have a larger radial coefficient of thermal contraction than the end can or coils and therefore contract more during cooldown. This decreases the radial pressure in the end can, and results in less clamping of the coils. In other words, stress in the coils decreases during cooldown. The prestress loss may be estimated in simple models by setting the change in coil radius due to prestress equal to the change in radius of the coils during cooldown (αΔTR). These equations predict that approximately 80% of the original prestress is lost during cooldown (49.7 and 51.7 MPa according to thin- and thick-walled cylinder theory respectively). The finite element model shows less prestress loss, (38% or 24.4 MPa), because it accounts for the contraction of the end can.
Prestress Loss During Magnetic Excitation. The magnetic field is three dimensional in the end clamp region and this complicates the determination of Lorentz forces. To simplify the problem, Lorentz forces are approximated using the straight section coil geometry in the dominant dipole field of 4.8 T (at 38.1 mm from the end of the straight section). Because the Lorentz forces are non uniformly distributed in both the
radial and azimuthal directions, models based on the thin-walled and thick walled cylinder equations are less simple to apply. The finite element model is used to predict coil stresses in a dipole field of 4.8T. Results are plotted in Figure 6. The average outer coil pole prestress decreases 16.5 MPa (2400 psi); the outer coil midplane stress increases 10.8 MPa (1500 psi). The average inner coil pole prestress decreases 25.5 MPa (3700 psi); the outer coil midplane stress increases 14.9 MPa (2200 psi).
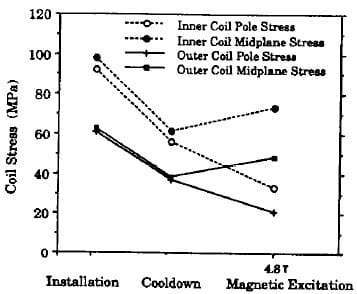
Figure 6. Coil Stress at Assembly, Cooldown, Excitation
Conclusions
The end clamps on 50mm aperture SSC Dipoles have performed successfully. No quenches have occurred in the end region of magnets whose end can diameter increased by 0.10 mm or more during installation onto the coils. Two training quenches have occurred in magnets whose end can diameter deflection was less than 0.10 mm and it is still not clear that these quenches were related to lower than average prestress.
To understand the data from Fermilab full length and model SSC Collider Dipole magnets, the mechanics of the end clamp assembly process were modeled as thin-walled cylinders, thick-walled cylinders, and with a finite element model. The results obtained, namely the end can diameter deflection, agreed within an order of magnitude with the averaged measured diameter deflection of nine full length and four model magnet end clamp assemblies after installation on the coil ends. The outer coil prestress input to all three models was 64 MPa (9300 psi), based on measurements made on test coils instrumented with pressure-sensitive tape. For this prestress the finite element model predicts relatively large prestress losses during cooldown and magnetic excitation. The prestress loss during cooldown could be reduced by using collet quadrants which have a smaller coefficient of thermal contraction in the radial direction. Some effort has been made to manufacture such collets by compression molding EM7302, and glass fiber filled epoxy. However, part tolerances could not be maintained.
References
- Delchamps, S.W., et al., SSC Collider Dipole Magnet End Mechanical Design, Proceedings of 1991 IEEE Particle Accelerator Conference, May 6-9, p. 2185, San Francisco, CA
- Koska, W.,et al., Tests of 40mm SSC Dipole Model Magnets with Vertically Split Yokes, Proceedings of 1991 IEEE Particle Accelerator Conference, May 6-9, San Francisco, CA
- Wake, M., et al., Tests of 1.5 Meter Model 5Onu-n SSC Collider Dipoles at Fermilab, Proceedings of 1991 IEEE Particle Accelerator Conference, May 6-9, San Francisco, CA
- Lamm, M., et al., Test Results from 5Omm Aperture, 15M long SSC Dipole Magnets at Fermilab, Fourth Annual International Industrial Symposium on the Super Collider, March 1992, New Orleans, LA
- Orris, D., et al., Quench Performance of Fermilab/General Dynamics Build Full Length SSC Collider Dipole Magnets, Fourth Annual International Industrial Symposium on the Super Collider, March 1992, New Orleans, LA
- Orrell, D., Magnetic Analysis and Design of End-Turns, MD-TA-181, SSCL, June 13,1991
- Delchamps, S., End Clamp Deflection for DCA311-DCA319, TS-SSC 92-013, Fermilab, January 29,1992
- Delchamps, S., Calibration of Fuji Prescale Pressure Sensitive Film, TS-SSC 91-134, Fermilab, July 8,1991
- Delchamps, S., Fuji Film Tests on DSA322 End Clamp Pressure, TS-SSC 91-135, Fermilab, July 2,1991
- Kerby, J., Finite Element Analysis of the End Collet Mechanism, TS-SSC 90-085, Fermilab, November 6,199O


