G A Matricali¹*, L Labey², W Bartels², G Dereymaeker², F P Luyten³, and J Vander Sloten²
*Corresponding author: Division of Orthopaedics, UZ Leuven, Katholieke Universiteit Leuven, Campus Pellenberg, Weligerveld 1, Leuven, Pellenberg, B-3212, Belgium. email: [email protected]
¹Division of Musculoskeletal Disorders, Katholieke Universiteit Leuven, Leuven, Belgium
²Division of Biomechanics and Engineering Design, Katholieke Universiteit Leuven, Leuven, Belgium
³Division of Rheumatology, Department of Musculoskeletal Sciences, Katholieke Universiteit Leuven, Leuven, Belgium
The manuscript was received on 18 December 2007 and was accepted after revision for publication on 9 June 2008.
DOI: 10.1243/09544119JEIM389
Abstract
Sealed pressure-sensitive film is frequently used to record contact characteristics in physiological joints. However, the effect on the pressure-recording characteristics of sealing the film when used in these circumstances has never been studied. This study compares the coefficient of variation, the standardized coefficient of variation, the tangent and secant contact stress gradients, and the actual pressures between unsealed and sealed Fuji film, in a simplified physiological joint model with a full-thickness surface defect. Unsealed film and sealed film were loaded through a range of nominal loads and the resulting stains were analysed by use of custom-made macros for the ImageJ image-processing program. The coefficient of variation did not exceed 5.7 per cent (sealed film), and the standardized coefficient of variation did not exceed 1.8 per cent (unsealed and sealed film). Contact stress gradients did not differ significantly. The recorded pressure at the level of surface defects was always about 0.2MPa higher in the case of sealed film, and therefore predictable. It is concluded that sealing the film will not change the pressure-recording characteristics.
Keywords: pressure-sensitive film, sealing, repeatability, contact stress gradient detection
1 Introduction
Intra-articular incongruities are considered to be an important cause of early osteoarthritis, or at least of lasting complaints and functional impairments. Clinically present as step-offs in the hyaline cartilage layer, these incongruities can be caused both by intra-articular fractures and by various types of joint surface defect [1, 2]. Recently, promising methods to treat joint surface defects have been developed, such as autologous osteochondral grafts and autologous chondrocyte implantation. However, both methods rely on the use of a donor site located in a ‘lesser weight-bearing area’ of the index joint or of another (healthy) joint [3–8]. Donor sitemorbidity is increasingly reported and its long-term outcome is uncertain [5, 9, 10]. To minimize donor site morbidity, studies to locate the most appropriate lesser weight-bearing area are mandatory. Therefore, determining the change in contact characteristics caused by intraarticular incongruities remains an important issue in biomechanical research.
Although some new methods are promising, Fuji pressure-sensitive film (FF) remains the technique of choice to perform this research. In particular, when the focus is on local detail, FF has its place [11]. Considering its thickness and E modulus, inserting FF into a joint space will inevitably change the various contact characteristics [12–14]. Furthermore, the presence of body fluids interferes with the stain-producing mechanism, indicating the need to produce fluid-proof packets [15]. Sealing will inevitably render the film stiffer and less able to adapt to joint surface incongruities, but only two papers have reported on the possible effects on repeatability and pressure-recording characteristics, and the used bench-top characteristics do not resemble those found in a physiological joint [12, 15]. Indeed, Hale and Brown [12] advised investigators using other grades of FF or targeting another application, to perform their own bench-top studies.
To the present authors’ knowledge, this is the first formal report on the performance of sealed FF in a model simulating a physiological joint with the presence of a joint surface defect. The goal of the present study was to compare the coefficient of variation (COV), the recorded contact stress gradients, and the recorded pressures for unsealed and sealed FF in a simplified physiological joint model. The study hypothesis was that sealing the FF would not importantly change the recording characteristics.
2 Materials and Methods
2.1 Physiological joint model
A simplified tibiotalar joint model was constructed. The bony component was represented by a rigid body, the cartilage by a layer 2mm thick of natural rubber (Luna Para; Eriks Belgium, Antwerp, Belgium; the manufacturer estimated the hardness to be approximately Shore 40 A), glued on the curved surface of the former. The choice of rubber was based on earlier reports [16, 17] and is in agreement with the results of the present authors’ preliminary tests (tensile E modulus, Luna Para, 1.06 MPa; unconfined compression E modulus, Luna Para, 8.25 MPa; E modulus, ankle joint cartilage ranges, 0.25–20.4MPa [18–21]).
The model consisted of two parts: a convex part and a concave part. The parts were 39 mm long, and 35 mm wide and had a radius of 31 mm [22–24]. A full-thickness defect was created in the rubber layer centrally on the apex of the convex component, sized 12 mm x 7 mm[25, 26], with the long axis of the defect perpendicular to the long axis of the component. To create reference points on the stains resulting from the experiments, four small beads (diameter, 0.8mm) were nearly completely sunk into the rubber layer of the convex component.
To prevent imprecise repositioning of both components, they were glued to a base plate to be clamped in the testing machine, in order to obtain a uniaxial movement in distraction–compression. Between the components and the base plate a compliant layer was added to reduce eccentric loading effects. To overcome a different amount of creep of rubber into the defect at higher loads, with differing defect sizes when comparing unsealed and sealed film, a second convex component was made entirely of the same metal as the rigid body, with the aforementioned surface defect machined.
2.2 Testing machine and loading regimen
All tests were performed on an Instron 4505 universal testing machine with a 100 kN load cell (Instron, Norwood, Massachusetts, USA). The loading regimen consisted of a preload of nominally 5 N, a 1 min linear ramp up to the de
sired nominal load, a 1 min hold at nominal load, and a 1min linear ramp down to the initial preload. Six different loads (400 N, 800 N, 1200 N, 2000 N, 3200 N, and 4000 N) were applied, corresponding to a range of loads from 0.5 to 5 times the body weight of a 80 kg individual.
2.3 Choice, preparation, and analysis of the pressure-sensitive film
As pressure-sensitive film, Fuji Prescale Film (Fuji Photo Film Co., Tokyo, Japan) was selected. Preliminary tests showed that super low film (LLW; 2 sheets type; range, 0.5–2.5MPa) best covered the pressure range obtained. Tegaderm® (3M, St Paul, Minnesota, USA) was used as sealing agent (polyurethane membrane coated with a layer of an acrylic adhesive, double-layer thickness, 0.095mm). Preparation of the FF and construction of the sealed units were carried out as described by Liggins et al. [15]. Temperature and relative humidity (RH) were checked regularly during testing and the test cycle was aborted for changes exceeding ±3 °C or ±3 per cent RH. If artefacts were immediately apparent to the naked eye, the stain was discarded and a new loading cycle performed. Because of the time restraints on Instron machine use, the stains were digitized 30 h after development. The C-film was scanned in 8-bit grey values at 300 dots/in, creating pixel values between 255 (completely white; unstained on the film) and 0 (completely black). Scanning was performed with a HP scanjet 2200C flat-bed scanner (Hewlett–Packard, Palo Alto, California, USA). Digital images were further stored and analysed on a personal computer running ImageJ, version 1.35 i (NIH, USA). To perform all analyses, custom-made macros were used.
To study the repeatability of sealed FF, the COV (per cent) (=[standard deviation (SD)/mean] x 100) and the standardized coefficient of variation (SCV)(per cent)(= COV (per cent)/[(population SD x 4)/mean]) of the mean pixel value of the stains were calculated. Tests were performed in triplicate using both types of convex component. The mean pixel value was obtained from a standardized rectangular region of interest, 252 pixels wide and 385 pixels long. This rectangle was positioned uniformly on the stain using the upper-left tantalum bead or the centre of the defect as reference point, in the case of the rubber-lined part and the full metal convex part, respectively (upper-left corner of the rectangle positioned 15 pixels under the centre of the mark of the bead, or the centre of the region of interest positioned at the centre of the defect) (Fig. 1).

Fig. 1 Representative stains obtained by loading unsealed super low-grade FF,
using the physiological joint model with both convex components (covered by rubber
and the full metal convex component), respectively. The position of the region of
interest used to determine the mean pixel value is shown: the upper-left corner of
the rectangle is positioned 15 pixels under the centre of the mark of the bead, or
the centre of the region of interest is positioned at the centre of the defect
The contact stress gradient detection and the recorded pressure at the centre of the defect were determined using five sets of test cycles performed in duplicate using the full metal convex component. The pressure gradient pattern at the edge of the defect was determined by scanning the stain perpendicular to the long axis of the defect over a length of 100 pixels before and 100 pixels beyond the defect. To minimize pixel-to-pixel variation, ensemble averaging [12] was performed using the centre 65 pixels lying along the x axis. All pressures were calculated by means of the equation describing the corresponding calibration curve.
The maximum detectable gradient was quantified in two numbers, in accordance with the work of Hale and Brown [12]. The first is the local derivative of the pressure profile and is called the ‘tangent gradient’; the second is the slope of a line connecting two extrema in the pressure profile and is called the ‘secant gradient’.
The maximum gradients detected in each test were calculated in the MATLAB programming environment (The Mathworks, Natick, Massachusetts, USA). First, the pressure profiles calculated from the ensemble-averaged pixel grey values were read in. Pressure values over 3.0MPa were discarded. Tangent gradients were calculated from the remaining pressure data as finite differences between subsequent pixels. The defect region, which was easily identifiable from the pressure profile, was isolated by manual selection; the minimum and the two maxima were detected automatically. Secant gradients were calculated from two lines connecting the minimum with the maxima.
2.4 Creation of a calibration curve and calculation of the recorded pressures
For each new test cycle, a corresponding calibration curve was created. Therefore, unsealed FF and sealed FF were exposed to 13 different loads corresponding to a pressure range 0.25–3 MPa. The calibration device consisted of a baseplate and a punch (diameter, 24.3mm) with a very finely polished surface, mounted on the Instron machine as mentioned above with the use of a baseplate and a compliant layer in between. After exposure, the developed stains were handled as already mentioned. The region of interest in the stain consisted of a circle with a diameter equal to that of the punch, located with its centre at the centre of the stain. The calibration curve was constructed by fifth-order polynomial regression [27]; the coefficients of the corresponding equation were calculated using the REGRP function of the matrix linear algebra package for Excel, MATRIX.XLA Ver1.6 (Foxes team, Rome, Italy).
2.5 Statistical analysis
Comparison of both pressure gradients between unsealed FF and sealed FF was made by the twotailed paired-sign test. P values less than 0.05 were considered significant. The SPSS statistical software program (SPSS Inc., Chicago, Illinois, USA) was used.
3 Results
Figure 1 shows representative stains obtained by loading unsealed film using both convex components. The COV and SCV calculated for both types of set-up are shown in Table 1. Considering all values, the highest COV was 5.7 per cent, and the highest SCV was 1.8 per cent.
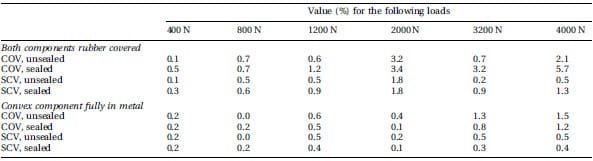
Table 1 COV and SCV values obtained after loading of super low-grade FF. The film was loaded in a physiological joint model consis
ting of a convex and a concave component. All tests were made in triplicate
Figure 2(a) shows a representative pressure profile measured across the centre of the defect. Sealed film shows a trend to record a slightly higher pressure than unsealed film does, but the pressure lines register the same shape of pressure profile. The calculated contact stress gradients are shown in Table 2. Comparison between unsealed film and sealed film yielded p=0.063 for the tangent gradient and p=0.375 for the secant gradient. At the centre of the defect, the pressure never fell to zero and increased consistently with increasing load. Sealed film did record higher pressures than unsealed film consistently, but the difference was shown to be constant at about 0.2 MPa (Fig. 2(b)).
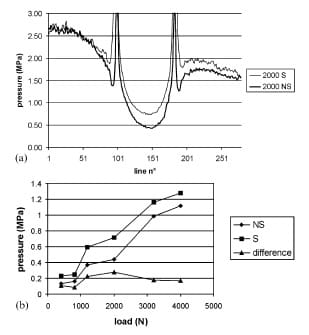
Fig. 2 (a) Representative pressure profile measured across the centre of the defect
while loading the full metal convex component of the physiological joint model (S,
sealed film; NS, unsealed film). (b) Contact pressure measured at the centre of the defect
(S, sealed film; NS, unsealed film). The sealed film recorded higher pressures than the unsealed
film consistently, but the difference was shown to be constant at about 0.2 MPa

Table 2 Calculated maximum tangent and secant contact stress gradients after loading
of super low-grade FF. The film was loaded unsealed and sealed in a physiological joint
model consisting of a convex and a concave component
4 Discussion
In this study, the authors were able to demonstrate that super low-grade FF, sealed with Tegaderm® shows an acceptable COV and SCV when tested in a set-up with a curved surface and a layer of compliant material at the contact area. At every nominal load, these values are in the same range as those of unsealed film. Concerning the contact stress gradients, no statistical difference could be detected. Furthermore, sealed film yields a pressure profile of a similar shape to that resulting from unsealed film at the level of a full-thickness surface defect. However, sealed film consistently registers a slightly higher nominal pressure, but the difference can be considered constant.
Some limitations of this study are evident. First, although the compliant layer simulating the articular cartilage was chosen to match the biomechanical properties of the latter, these properties were not taken into account when choosing the material for the rigid body. Second, the contact surface was curved in only one direction. However, a multi-axial curved surface would have induced inevitable crinkle artefacts, making the exact analysis of the stains much more difficult or even unreliable. Third, considering the need for an actual defect of fixed size when testing at different nominal loads with both unsealed and sealed film, it was necessary to use a full metal convex component for certain tests.
A maximum COV of 5.7 per cent was found, using sealed film at the highest load regimen. All other COVs in this set-up did not exceed 3.4 per cent. When testing the full metal convex component, the maximum COV was 1.5 per cent. In all the test series, the COV showed a trend of higher values at higher loads, as also observed by Liggins et al. [15]. This can easily be explained: at higher loads the corresponding mean pixel value will be lower and, therefore, the same absolute error will result in a higher COV. Therefore, the SCV was also calculated and was shown to be relatively constant, indicating an equal repeatability of the film itself at each load. However, it is acknowledged that equivalence of variation was not proved. Such proof would, depending on the specific definition of an ignorable difference in variation, and based on a power analysis, need a number of replications beyond practical limitations. Therefore, only the observed indices of variability were reported, to explore if they are in a comparable range.
Furthermore, the contact stress gradients and the pressure profile of unsealed FF and sealed FF were compared. Although a trend for sealed film to have a lower tangent contact stress gradient was present, the difference has no proven statistical significance. The secant contact stress gradient did not show a significant difference either. Similarly shaped pressure profile plots were observed, although the sealed film showed a trend to record a slightly higher pressure. Recording a pressure at the level of the defect is highly suggestive for direct physical contact between the intact rubber layer of the concave component and the bottom of the defect. Incursion of rubber in the defect can be explained by concomitant deformation of the edges of the defect and of the overlying intact surface of the concave component. Such a phenomenon is reported to occur when modelling step-offs of the tibial plateau, and when loading rabbit knees [28, 29]. However, even if a formal contact at the bottom of the defect is not present, the smallest amount of incursion will create a load upon the interjacent FF unit that will be recorded as a certain amount of pressure. The recorded pressures at the centre of the defect were consistently higher by 0.2 MPa for sealed film. This can probably be explained by the higher stiffness of the sealed units of film, which requires a greater force to bend the film into the defect. Nevertheless, the constant value of this effect makes it predictable.
It is concluded that the repeatability and contact stress gradient detection of sealed units of super low-grade FF can be considered similar to those of unsealed film, when used at a curved contact area and in the presence of a full-thickness surface defect. However, considering the already reported influence on the recorded pressures by inserting FF in articular joints [13], care has to be taken when interpreting the obtained results.
Acknowledgements
The authors thank Jo Marie¨n, Bart Pelgrims, and Kris Van De Staey of the Department of Metallurgy and Materials Engineering, Katholieke Universiteit Leuven, for their technical assistance. G. Van der Perre is gratefully acknowledged for his help when initiating this study, Jeroen De Wachter for his help when searching for the appropriate compliant material, and Steffen Fieuws for his invaluable statistical advice. Thanks are due to Elvire Helsemans and Alfonsina Fini for their secretarial support. This study was supported in part by the Clinical Research Fund of
the Universitaire Ziekenhuizen Leuven. The Tegaderm® was kindly provided by 3M Europe NVSA, Diegem (Belgium). The authors declare that no other conflicts of interest exist.
References
- Hunziker, E. B. Articular cartilage repair: basic science and clinical progress. A review of the current status and prospects. Osteoarthritis Cartilage, 2001, 10, 432–463.
- Thomas, R. H. and Daniels, T. R. Current concepts review ankle arthritis. J. Bone Jt Surg. Am., 2003, 85(5), 923–936.
- Brittberg, M., Lindahl, A., Nilsson, A., Ohlsson, C., Isaksson, O., and Peterson, L. Treatment of deep cartilage defects in the knee with autologous chondrocyte transplantation. N. Engl. J. Medicine, 1994, 331(14), 889–895.
- Hangody, L., Kish, G., Ka´rpa´ti, Z., Szerb, I., and Udvarhelyi, I. Arthroscopic autogenous osteochondral mosaicplasty for the treatment of femoral condylar articular defects, a preliminary report. Knee Surg., Sports Traumatology, Arthroscory, 1997, 5, 262–267.
- Bartha, L., Vajda, A., Duska, Z., Rahmeh, H., and Hangody, L. Autologous osteochondral mosaicplasty grafting. J. Orthop. Sports Phys. Therapy, 2006, 36(10), 739–750.
- Vanlauwe, J., Almqvist, K. F., Bellemans, J., Huskin, J.-P., Verdonk, R., and Victor, J. Repair of symptomatic cartilage lesions of the knee. The place of autologous chondrocyte implantation. Acta Orthop. Belg., 2007, 73, 145–158.
- Giannini, S., Buda, R., Vannini, F., Di Caprio, F., and Grigolo, B. Arthroscopic autologous chondrocyte implantation in osteochondral lesions of the talus. Am. J. Sports Medicine, 2008, 36(5), 873–880.
- Aurich, M., Venbrocks, R. A., and Fuhrmann, R. A. Autologe chondrozyten-transplantation am oberen sprunggelenk. Rational oder irrational? Orthopa¨de, 2008, 37(3), 188–195.
- Whittaker, J.-P., Smith, G., Makwana, N., Roberts, S., Harrison, P. E., Laing, P., and Richardson, J. B. Early results of autologous chondrocyte implantation in the talus. J. Bone Jt Surg. Am., 2005, 87, 179–183.
- Reddy, S., Pedowitz, D. I., Parekh, S. G., Sennett, B. J., and Okereke, E. The morbidity associated with osteochondral harvest from asymptomatic knees for the treatment of osteochondral lesions of the talus. Am. J. Sports Medicine, 2007, 35(1), 80–85.
- Brown, T. D., Rudert, M. J., and Grosland, N. M. New method for assessing cartilage contact stress after articular fracture. Clin. Orthop. Related Res., 2004, 423, 52–58.
- Hale, J. E. and Brown, T. D. Contact stress gradient detection limits of pressensor film. J. Biomech. Engng, 1992, 114, 352–357.
- Wu, J. Z., Herzog, W., and Epstein, M. Effects of inserting a pressensor film into articular joints on the actual contact mechanics. J. Biomech. Engng, 1998, 120, 655–659.
- Liau, J. J., Cheng, C. K., Huang, C. H., and Lo, W. H. Effect of Fuji pressure sensitive film on actual contact characteristics of artificial tibiofemoral joint. Clin. Biomechanics, 2002, 17, 698–704.
- Liggins, A. B., Surry, K., and Finlay, J. B. Sealing Fuji Prescale pressure sensitive film for protection against fluid damage: the effect on its response. Strain, 1995, 31(2), 57–62.
- Simon, W. H. Scale effects in animal joints; II thickness and elasticity in the deformability of articular cartilage. Arthritis Rheum., 1971, 14(4), 493–502.
- Caldwell, N. J., Hale, J. E., Rudert, M. J., and Brown, T. D. An algorithm for approximate crinkle artefact compensation in pressure-sensitive film recordings. J. Biomechanics, 1993, 26(8), 1001–1009.
- Athanasiou, K. A., Niederauer, G. G., and Schenck, R. C. Biomechanical topography of human ankle cartilage. Ann. Biomed. Engng, 1995, 23, 697–704.
- Shepherd, D. E. T. and Seedhom, B. B. The ‘instantaneous’ compressive modulus of human articular cartilage in joints of the lower limb. Rheumatology, 1999, 38, 124–132.
- Treppo, S., Koepp, H., Quan, E. C., Cole, A. A., Kuettner, K. E., and Grodzinsky, A. J. Comparison of biomechanical and biochemical properties of cartilage from human knee and ankle pairs. J. Orthop. Res., 2000, 18, 739–748.
- Seog, J., Dean, D., Rolauffs, B., Wu, T., Genzer, J., Plaas, A. H., Grodzinsky, A. J., and Ortiz, C. Nanomechanics of opposing glycosaminoglycan macromolecules. J. Biomechanics, 2005, 38(9), 1789–1797.
- Thoma, W., Scale, D., and Kurth, A. Computergestu ¨tze analyse der kinematik des oberen sprunggelenks. Z. Orthop., 1993, 131, 14–17.
- Fessy, M. H., Carret, J. P., and Be´jui, J. Morphometry of the talocrural joint. Surg. Radiologic Anat., 1997, 19, 299–302.
- Leardini, A., O’Connor, J. J., Catani, F., and Giannini, S. A geometric model of the human ankle joint. J. Biomechanics, 1999, 32, 585–591.
- Christensen, J. C., Driscoll, H., and Tencer, A. F. Contact characteristics of the ankle joint. Part 2. The effects of talar dome cartilage defects. J. Am. Podiatric Med. Assoc., 1994, 84(11), 537–547.
- Matricali, G. A., Dereymaeker, G. Ph. E., and Luyten, F. P. The postero-medial rim of the talar dome as the site to harvest cartilage in the ankle: an anatomic study. Arthroscopy, 2006, 22(11), 1241–1245.
- Liggins, A. B., Hardie, W. R., and Finlay, J. B. The spatial and pressure resolution of Fuji pressuresensitive film. Expl Mechanics, 1995, 35(2), 166–173.
- Huber-Betzer, H., Brown, T. D., Mattheck, C., and Aberman, H. M. Some effects of global joint morphology on local stress aberrations near imprecisely reduced intra-articular fractures. J. Biomechanics, 1990, 23(8), 811–822.
- Braman, J. P., Bruckner, J. D., Clark, J. M., Norman, A. G., and Chansky, H. A. Articular cartilage adjacent to experimental defects is subject to atypical strains. Clin. Orthop. Related Res., 2005, 430, 202–207.


